题目内容
已知函数y=| 1 |
| 2 |
| π |
| 6 |
(1)求它的振幅、周期、初相;
(2)用五点法作出它的简图;
(3)该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
分析:(1)分别令
+
取0,
,π,
,2π,并求出对应的(x,d(x))点,描点后即可得到函数在一个周期内的图象
(2)根据函数的解析式中A=3,ω=
,φ=
,然后根据正弦型函数的性质,即可求出f(x)的周期、振幅、初相、对称轴;
(3)根据正弦型函数的平移变换,周期变换及振幅变换的法则,根据函数的解析式,易得到函数图象可由y=sinx在[0,2π]上的图象经怎样的变换得到的.
| x |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 3π |
| 2 |
(2)根据函数的解析式中A=3,ω=
| 1 |
| 2 |
| π |
| 6 |
(3)根据正弦型函数的平移变换,周期变换及振幅变换的法则,根据函数的解析式,易得到函数图象可由y=sinx在[0,2π]上的图象经怎样的变换得到的.
解答:解:(1)函数y=
sin(2x+
)的振幅为
,周期为π,初相为
.
(2)列表:
画简图: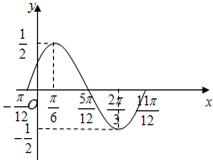
(3)
函数y=sinx的图象向左平移
个单位,得到
函数y=sin(x+
)的图象,再保持纵坐标不变,把横坐标缩短为原来的一半得到函数y=sin(2x+
)的图象,再保持横坐标不变,把纵坐标缩短为原来的一半得到函数y=
sin(2x+
)的图象.
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
(2)列表:
| x | -
|
|
|
|
| ||||||||||
2x+
|
0 |
|
π |
|
2π | ||||||||||
y=
|
0 |
|
0 | -
|
0 |

(3)
函数y=sinx的图象向左平移
| π |
| 6 |
函数y=sin(x+
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
点评:本题考查的知识点是五点法作函数y=Asin(ωx+φ)的图象,函数y=Asin(ωx+φ)的图象变换,其中正弦型函数的图象的画法,性质是三角函数的重点内容之一,一定要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目