题目内容
规定A![]() =x(x-1)…(x-m+1),其中x∈R,m为正整数,且A
=x(x-1)…(x-m+1),其中x∈R,m为正整数,且A![]() =1,这是排列数A
=1,这是排列数A![]() (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.
(1)求A![]() 的值;
的值;
(2)排列数的两个性质:①A![]() =nA
=nA![]() ,②A
,②A![]() +mA
+mA![]() =A
=A![]() (其中m,n是正整数).是否都能推广到A
(其中m,n是正整数).是否都能推广到A![]() (x∈R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(x∈R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(3)确定函数A![]() 的单调区间.
的单调区间.
见解析
解析:
解:(1)![]() =(-15)(-16)(-17)= - 4080;
=(-15)(-16)(-17)= - 4080;
(2)性质①、②均可推广,推广的形式分别是
①![]() ,②
,②![]() (x∈R,m∈N+)
(x∈R,m∈N+)
事实上,在①中,当m=1时,左边=![]() =x,右边=x
=x,右边=x![]() =x,等式成立;
=x,等式成立;
当m≥2时,左边=x(x-1)(x-2)…(x-m+1)=x{(x-1)(x-2)…[(x-1)-(m-1)+1]}=x![]() ,
,
因此,①![]() 成立;
成立;
在②中,当m=l时,左边=![]() +
+![]() =x+l=
=x+l=![]() =右边,等式成立;
=右边,等式成立;
当m≥2时,左边=x(x-1)(x-2)…(x-m+1)+mx(x-1)(x-2)…(x-m+2)
=x(x-1)(x-2)…(x-m+2)[(x-m+1)+m]
=(x+1)x(x-1)(x-2)…[(x+1)-m+1]=![]() =右边,
=右边,
因此②![]() (x∈R,m∈N+)成立.
(x∈R,m∈N+)成立.
(3)先求导数,得(![]() )/=3x2-6x+2.令3x2-6x+2>0,解得x<
)/=3x2-6x+2.令3x2-6x+2>0,解得x<![]() 或x>
或x>![]()
因此,当x∈(-∞,![]() )时,函数为增函数,当x∈(
)时,函数为增函数,当x∈(![]() ,+∞)时,函数也为增函数.
,+∞)时,函数也为增函数.
令3x2-6x+2≤0, 解得![]() ≤x≤
≤x≤![]() ,因此,当x∈[
,因此,当x∈[![]() ,
,![]() ]时,函数为减函数.
]时,函数为减函数.
∴函数![]() 的增区间为(-∞,
的增区间为(-∞,![]() ),(
),(![]() ,+∞);减区间为[
,+∞);减区间为[![]() ,
,![]() ].
].

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
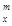 =x(x-1)…(x-m+1),其中x∈R,m为正整数,且A
=x(x-1)…(x-m+1),其中x∈R,m为正整数,且A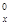 =1,这是排列数A
=1,这是排列数A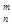 (n,m是正整数,且m≤n)的一种推广.
(n,m是正整数,且m≤n)的一种推广.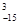 的值;
的值; (其中m,n是正整数).问是否都能推广到A
(其中m,n是正整数).问是否都能推广到A ,其中P、M是实数集R的两个非空子集,又规定A(P)={y|y=f(x),x
,其中P、M是实数集R的两个非空子集,又规定A(P)={y|y=f(x),x P},A(M)={y|y= f(x),x
P},A(M)={y|y= f(x),x M=
M= ,则A(P)
,则A(P)
 M=R,则A(P)
M=R,则A(P)