题目内容
8．已知函数y=x2+3x+1（x＞0）的图象在函数y=ax（x＞0）图象的上方，则参数a的取值范围是（ ）| A． | （-∞，5） | B． | （-∞，3$\sqrt{3}$） | C． | （-∞，5] | D． | （-∞，3$\sqrt{3}$] |
分析 问题转化为a≤x+$\frac{1}{x}$+3即可，通过基本不等式求出x+$\frac{1}{x}$+3的最小值，从而求出a的范围．
解答 解：若函数y=x2+3x+1（x＞0）的图象在函数y=ax（x＞0）图象的上方，
则只需x2+3x+1≥ax，即a≤x+$\frac{1}{x}$+3即可，
而x+$\frac{1}{x}$≥2，∴x+$\frac{1}{x}$+3的最小值是5，
故a≤5，
故选：C．
点评 本题考查了函数恒成立问题，考查基本不等式问题，是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
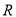的函数
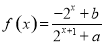是奇函数．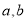
的值；
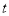的不等式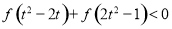
．
如图：已知矩形BB1C1C所在平面与底面ABB1N垂直，直角梯形ABB1N中AN∥BB1，AB⊥AN，CB=BA=AN=2，BB1=4．
中央电视台“星光大道”节目的现场观众来自4所学校，分别在图中的四个区域Ⅰ，Ⅱ，Ⅲ，Ⅳ坐定．有4种不同颜色的服装，同一学校的观众必须穿上同种颜色的服装，且相邻两个区域的颜色不同，不相邻区域颜色相同与否不受限制，那么不同着装方法有多少种？