Question

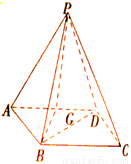
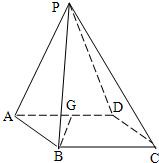20、P是四边形ABCD所在平面外一点，ABCD是∠DAB=60°且边长为a的菱形，侧面PAD为正三角形，其所在平面垂直于底面ABCD．
（1）若G为AD边的中点，求证：BG⊥平面APD；
（2）求证：AD⊥PB．

Answer 1

分析：（1）连接BD，根据条件可知△ABD是正三角形，而G为AD边的中点，则BG⊥AD，BG?平面ABCD又平面APD⊥平面ABCD，平面APD∩平面ABCD=AD，根据面面垂直的性质定理可知BG⊥平面APD；
（2）连接PG，由侧面PAD为正三角形，G为AD边的中点得到AD⊥PG，再由（1）可知BG⊥AD，PG，BG?平面PBG，PG∩BG=G，根据线面垂直的判定定理可知AD⊥平面PBG，而PB?平面PBG，根据线面垂直的性质可知AD⊥PB．

解答：证明：（1）连接BD，由已知∠DAB=60°且四边形ABCD是菱形∴△ABD是正三角形，又G为AD边的中点
∴BG⊥AD，BG?平面ABCD又平面APD⊥平面ABCD，平面APD∩平面ABCD=AD，∴BG⊥平面APD
（2）连接PG，由侧面PAD为正三角形，G为AD边的中点∴AD⊥PG
由（1）可知BG⊥AD，PG，BG?平面PBG，PG∩BG=G∴AD⊥平面PBG，又PB?平面PBG∴AD⊥PB．

点评：本小题主要考查直线与平面垂直的判定，以及线面垂直的性质等有关知识，考查空间想象能力、运算能力和推理论证能力，考查转化思想，属于基础题．