题目内容
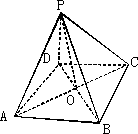
如图，P是四边形ABCD所在平面外的一点，四边形ABCD是∠DAB=60°且边长为
的菱形，侧面PAD为正三角形，其所在的平面垂直于底面ABCD．若G为AD的中点，
⑴求证：BG⊥平面PAD；
⑵求PB与面ABCD所成角．
【答案】
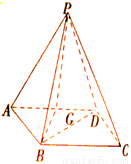
⑴连接BD，在菱形ABCD中，∠DAB=60°,故△ABD为正三角形,又G为ＡD的中点，所以，ＢG⊥ＡＤ．
△PAD为正三角形，G为AD的中点,所以，PG⊥AD 又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD＝AD，所以，ＰG⊥面ABD，故 PG⊥BG
所以，ＢG⊥平面PAD.
（2）易知△PBG为等腰直角三角形，可知PB与面ABCD所成角为45。
【解析】略
练习册系列答案
名校课堂系列答案
相关题目
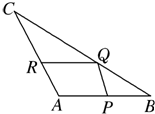如图，△ABC是一块边长AB=3m，AC=5m，BC=7m的剩余角料．现要从中裁剪出一块面积最大的平行四边形用料APQR，要求顶点P，Q，R分别在边AB，BC，CA上．问点Q在BC边上的什么位置时，剪裁符合要求？并求这个最大值．
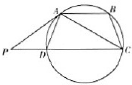如图，ABCD是圆的内接四边形，AB∥CD，过A点的圆的切线与CD的延长线交于P点，证明：
如图，ABCD是边长为2的正方形纸片，沿某动直线l为折痕将正方形在其下方的部分向上翻折，使得每次翻折后点B都落在边AD上，记为B'；折痕与AB交于点E，以EB和EB’为邻边作平行四边形EB’MB．若以B为原点，BC所在直线为x轴建立直角坐标系（如下图）：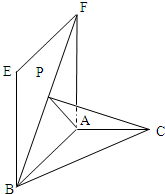
（2008•湖北模拟）如图，直二面角E-AB-C中，四边形ABEF是矩形，AB=2，AF=