题目内容
平面内与两定点![]() 连线的斜率之积等于常数
连线的斜率之积等于常数![]() (
(![]() 的点的轨迹,连同
的点的轨迹,连同![]() 两点所成的曲线为C.
两点所成的曲线为C.
(Ⅰ)求曲线C的方程,并讨论C的形状;
(II)设![]() ,
,![]() ,对应的曲线是
,对应的曲线是![]() ,已知动直线
,已知动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两不同点,且
两不同点,且![]() ,其中O为坐标原点,探究
,其中O为坐标原点,探究 ![]() 是否为定值,写出解答过程。
是否为定值,写出解答过程。
解:(Ⅰ)设动点为M,其坐标为![]() ,
,
当![]() 时,由条件可得
时,由条件可得![]()
即![]() ,又
,又![]() 的坐标满足
的坐标满足![]()
故依题意,曲线C的方程为![]()
当![]() 曲线C的方程为
曲线C的方程为![]() 是焦点在y轴上的椭圆;
是焦点在y轴上的椭圆;
当![]() 时,曲线C的方程为
时,曲线C的方程为![]() ,C是圆心在原点的圆;
,C是圆心在原点的圆;
当![]() 时,曲线C的方程为
时,曲线C的方程为![]() ,C是焦点在x轴上的椭圆; ……6分
,C是焦点在x轴上的椭圆; ……6分
(Ⅱ)解:![]() :
:![]()
当直线![]() 的斜率不存在时,P,Q两点关于x轴对称,
的斜率不存在时,P,Q两点关于x轴对称,
所以![]() 因为
因为![]() 在椭圆上,因此
在椭圆上,因此![]() ①
①
又因为![]() 所以
所以![]() ②
②
由①、②得![]() 此时
此时![]()
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]()
将其代入![]() ,得
,得![]() ,
,
其中![]() 即
即 ![]() (*)
(*)
又![]() ,
,![]()
所以![]()
因为点O到直线![]() 的距离为
的距离为![]() 所以
所以![]()
![]()
![]()
![]()
又![]() 整理得
整理得![]() 且符合(*)式,
且符合(*)式,
此时![]()
![]()
综上所述![]() 结论成立 ……13分
结论成立 ……13分
(Ⅱ)解法2: ![]()
![]()
令P![]() ,Q
,Q![]()
![]() 化简得
化简得![]()
又P![]() ,Q
,Q![]() 在
在![]()
则![]()
![]()
代入![]() 得
得![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
相关题目
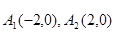 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数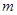 的点的轨迹,加上
的点的轨迹,加上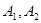 两点,所成的曲线
两点,所成的曲线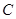 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.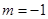 时,对应的曲线为
时,对应的曲线为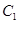 ;对给定的
;对给定的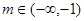 ,对应的曲线为
,对应的曲线为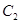 ,若曲线
,若曲线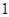 的切线与曲线
的切线与曲线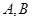 两点,且
两点,且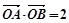 (
(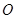 为坐标原点),求曲线
为坐标原点),求曲线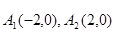 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数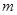 的点的轨迹,加上
的点的轨迹,加上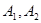 两点,所成的曲线
两点,所成的曲线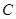 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.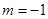 时,对应的曲线为
时,对应的曲线为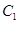 ;对给定的
;对给定的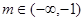 ,对应的曲线为
,对应的曲线为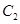 ,若曲线
,若曲线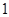 的切线与曲线
的切线与曲线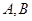 两点,且
两点,且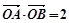 (
(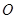 为坐标原点),求曲线
为坐标原点),求曲线 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数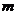 的点的轨迹,加上
的点的轨迹,加上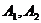 两点,所成的曲线
两点,所成的曲线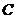 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.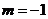 时,对应的曲线为
时,对应的曲线为 ;对给定的
;对给定的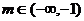 ,对应的曲线为
,对应的曲线为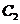 ,若曲线
,若曲线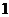 的切线与曲线
的切线与曲线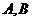 两点,且
两点,且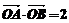 (
( 为坐标原点),求曲线
为坐标原点),求曲线