题目内容

 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=| π | 2 |
(1)写出f(x)表达式,并求f(x)的最大值;
(2)当x=2时,求异面直线AB与DF所成角θ的余弦值.
分析:(1)过D作DH∥AE,则DG=AE,且DH⊥平面EBCF,由f(x)=VD-BFC =
×S△BFC×DH 求出f(x)的解析式,
由二次函数的性质求出其最大值.
(2)过A作AG∥DF,连BG,则∠BAG即为异面直线AB与DF所成的角,求出此角所在三角形的三边长,余弦定理求得
θ的余弦值.
| 1 |
| 3 |
由二次函数的性质求出其最大值.
(2)过A作AG∥DF,连BG,则∠BAG即为异面直线AB与DF所成的角,求出此角所在三角形的三边长,余弦定理求得
θ的余弦值.
解答:解:(1)∵AE⊥平面EBCF,过D作DH∥AE,则DG=AE,且DH⊥平面EBCF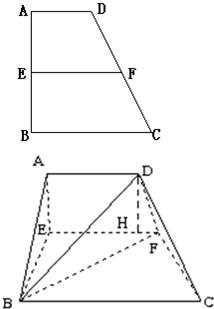 ,所以,
,所以,
f(x)=VD-BFC =
×S△BFC×DH=
×
×4×(4-x)×x
=-
(x-2)2+
≤
,
即x=2时,f(x)有最大值为
.
(2)过A作AG∥DF,连BG,则∠BAG即为异面直线AB与DF所成的角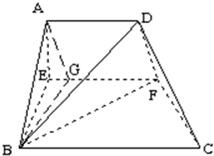
由x=2知EG=1,在△AEG中,AG2=22+12=5
在△BEG中,BG2=22+12=5,在△AEB中,AB2=22+22=8,
∴由余弦定理可得 cosθ=
=
.
 ,所以,
,所以,f(x)=VD-BFC =
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
=-
| 2 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
即x=2时,f(x)有最大值为
| 8 |
| 3 |
(2)过A作AG∥DF,连BG,则∠BAG即为异面直线AB与DF所成的角

由x=2知EG=1,在△AEG中,AG2=22+12=5
在△BEG中,BG2=22+12=5,在△AEB中,AB2=22+22=8,
∴由余弦定理可得 cosθ=
| 8+5-5 | ||||
2×
|
| ||
| 5 |
点评:本题考查求三棱锥的体积,求函数的最大值,求异面直线所成的角的余弦值,找出异面直线所成的角,是解题的
关键.
关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图,已知梯形ABCD中|AB|=2|CD|,点E分有向线段
如图,已知梯形ABCD中|AB|=2|CD|,点E分有向线段
 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD= 已知梯形ABCD中,AD∥BC,
已知梯形ABCD中,AD∥BC, 如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.
如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.