题目内容
 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=| π | 2 |
(1)当x=2时,求证:BD⊥EG;
(2)求f(x)的最大值;
(3)当f(x)取得最大值时,求异面直线AE与BD所成的角的余弦值.
分析:(1)作DH⊥EF,垂足H,连结BH、GH,根据面面垂直的性质证出DH⊥平面EBCF,从而EG⊥DH,根据题中数据结合EF∥BC,∠ABC=90°,证出四边形BGHE为正方形,得EG⊥BH,可得EG⊥平面DBH,从而得出EG⊥BD;
(2)根据面面垂直的性质证出AE⊥面EBCF,可得AE∥DH,从而得四边形AEHD是矩形,得DH=AE=x等于以F、B、C、D为顶点的三棱锥D-BCF的高.结合S△BCF=
BC•BE=8-2x,算出三棱锥D-BCF的体积为V=f(x)=
S△BFC•AE=
( 8-2x )x,在x=2时,f(x)有最大值为
;
(3)由(2)知当f(x)取得最大值时AE=2,故BE=2,结合DH∥AE得∠BDH是异面直线AE与BD所成的角.在Rt△BEH中,算出BH=2
,△BDH中,得到BD=2
,最后利用直角三角形中三角函数的定义,算出cos∠BDH=
=
,从而得到异面直线AE与BD所成的角的余弦值.
(2)根据面面垂直的性质证出AE⊥面EBCF,可得AE∥DH,从而得四边形AEHD是矩形,得DH=AE=x等于以F、B、C、D为顶点的三棱锥D-BCF的高.结合S△BCF=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
(3)由(2)知当f(x)取得最大值时AE=2,故BE=2,结合DH∥AE得∠BDH是异面直线AE与BD所成的角.在Rt△BEH中,算出BH=2
| 2 |
| 3 |
| DH |
| BD |
| ||
| 3 |
解答:解:(1)作DH⊥EF,垂足H,连结BH、GH,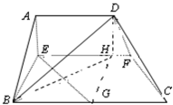
∵平面AEFD⊥平面EBCF,平面AEFD∩平面EBCF=EF,DH?平面EBCF,
∴DH⊥平面EBCF,结合EG?平面EBCF,得EG⊥DH,
∵EH=AD=
BC=BG,EF∥BC,∠ABC=90°.
∴四边形BGHE为正方形,得EG⊥BH.
又∵BH、DH?平面DBH,且BH∩DH=H,∴EG⊥平面DBH.
∵BD?平面DBH,∴EG⊥BD.
(2)∵AE⊥EF,平面AEFD⊥平面EBCF,平面AEFD∩平面EBCF=EF,AE?平面AEFD.
∴AE⊥面EBCF.结合DH⊥平面EBCF,得AE∥DH,
∴四边形AEHD是矩形,得DH=AE,
故以F、B、C、D为顶点的三棱锥D-BCF的高DH=AE=x,
又∵S△BCF=
BC•BE=
×4×( 4-x )=8-2x.
∴三棱锥D-BCF的体积为V=f(x)=
S△BFC•DH=
S△BFC•AE
=
( 8-2x )x=-
x2+
x=-
(x-2)2+
≤
.
∴当x=2时,f(x)有最大值为
.
(3)由(2)知当f(x)取得最大值时AE=2,故BE=2,
结合DH∥AE,可得∠BDH是异面直线AE与BD所成的角.
在Rt△BEH中,BH=
=
=2
,
∵DH⊥平面EBCF,BH?平面EBCF,∴DH⊥BH
在Rt△BDH中,BD=
=
=2
,
∴cos∠BDH=
=
=
.
∴异面直线AE与BD所成的角的余弦值为
.

∵平面AEFD⊥平面EBCF,平面AEFD∩平面EBCF=EF,DH?平面EBCF,
∴DH⊥平面EBCF,结合EG?平面EBCF,得EG⊥DH,
∵EH=AD=
| 1 |
| 2 |
∴四边形BGHE为正方形,得EG⊥BH.
又∵BH、DH?平面DBH,且BH∩DH=H,∴EG⊥平面DBH.
∵BD?平面DBH,∴EG⊥BD.
(2)∵AE⊥EF,平面AEFD⊥平面EBCF,平面AEFD∩平面EBCF=EF,AE?平面AEFD.
∴AE⊥面EBCF.结合DH⊥平面EBCF,得AE∥DH,
∴四边形AEHD是矩形,得DH=AE,
故以F、B、C、D为顶点的三棱锥D-BCF的高DH=AE=x,
又∵S△BCF=
| 1 |
| 2 |
| 1 |
| 2 |
∴三棱锥D-BCF的体积为V=f(x)=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
∴当x=2时,f(x)有最大值为
| 8 |
| 3 |
(3)由(2)知当f(x)取得最大值时AE=2,故BE=2,
结合DH∥AE,可得∠BDH是异面直线AE与BD所成的角.
在Rt△BEH中,BH=
| BE2+EH2 |
| 4+AD2 |
| 2 |
∵DH⊥平面EBCF,BH?平面EBCF,∴DH⊥BH
在Rt△BDH中,BD=
| BH2+DH2 |
| 8+AE2 |
| 3 |
∴cos∠BDH=
| DH |
| BD |
| 2 | ||
2
|
| ||
| 3 |
∴异面直线AE与BD所成的角的余弦值为
| ||
| 3 |
点评:本题给出平面折叠问题,求证直线与直线垂直,求体积的最大值并求此时异面直线所成角大小.着重考查了面面垂直的性质定理、线面垂直的判定与性质和异面直线所成角大小的求法等知识,属于中档题.

练习册系列答案
相关题目
 如图,已知梯形ABCD中|AB|=2|CD|,点E分有向线段
如图,已知梯形ABCD中|AB|=2|CD|,点E分有向线段
 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD= 如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.
如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.