题目内容
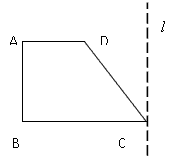
如图，已知梯形ABCD中，AD∥BC，∠ABC=90°，AD=a，BC=2a，∠DCB=60°，在平面ABCD内，过C作l⊥CB，以l为轴将梯形ABCD旋转一周，求所得旋转体的表面积及体积．分析：根据该旋转体的外形分析其结构可得，它是在一个底面半径为2a、高为
a的圆柱中挖去一个底面半径为a、高为
a的圆锥，由此不难请计算出它的表面积和体积．
| 3 |
| 3 |
解答：解：由题意，线段AB旋转一周形成圆柱的侧面，线段CB旋转一周形成圆C，CD旋转一周形成圆锥的侧面，线段AD旋转一周形成一个圆环，
∵∠DCB=60°，∴圆锥的底面半径为r=a，母线l=2a，高为
a
∴旋转体的表面积S=S圆柱侧+S圆C+S圆锥侧+S圆环=2π•2a•
a+π•（2a）2+π•a•2a+π[（2a）2-a2]=(9+4
)πa2…（7分）
该旋转体的体积是经AB为母线的圆柱体积减去以CD为母线的圆锥的体积，即
V=π•（2a）2•
a-
π•a2•
a=
πa3…（14分）
∵∠DCB=60°，∴圆锥的底面半径为r=a，母线l=2a，高为
| 3 |
∴旋转体的表面积S=S圆柱侧+S圆C+S圆锥侧+S圆环=2π•2a•
| 3 |
| 3 |
该旋转体的体积是经AB为母线的圆柱体积减去以CD为母线的圆锥的体积，即
V=π•（2a）2•
| 3 |
| 1 |
| 3 |
| 3 |
| 11 |
| 3 |
| 3 |
点评：本题给出一个特殊的旋转体，要我们求的表面积与体积，着重考查了圆柱、圆锥的侧面积和体积等公式，属于基础题．
练习册系列答案
字词句段篇系列答案
相关题目
＝λ
(λ∈R，λ＞0)．
时，求证：GM∥平面DFN．
，试求二面角M－BC－D的余弦值．
为矩阵
属于λ的一个特征向量，求实数a，λ的值及A2。
（α为参数），曲线D的参数方程为
，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。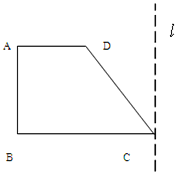
如图，已知梯形ABCD中，AD∥BC，∠ABC=90°，AD=a，BC=2a，∠DCB=60°，在平面ABCD内，过C作l⊥CB，以l为轴将梯形ABCD旋转一周，求所得旋转体的表面积及体积．