题目内容
 (2011•广东三模)已知函数f(x)=2sinx(sinx+cosx)-1.
(2011•广东三模)已知函数f(x)=2sinx(sinx+cosx)-1.(1)求函数f(x)的最小正周期和最大值;
(2)在给定的坐标系内,用五点作图法画出函数f(x)在一个周期内的图象.
分析:(1)先利用二倍角公式和两角差的正弦公式将函数化简为y=Asin(ωx+φ)的形式,利用周期公式求其最小正周期,利用函数图象和性质求其最大值
(2)先将内层函数ωx+φ看作整体,取正弦函数的五个关键点横坐标值,列出函数取值表,再依表描点,用平滑的曲线将其连接即可得函数f(x)在一个周期内的图象
(2)先将内层函数ωx+φ看作整体,取正弦函数的五个关键点横坐标值,列出函数取值表,再依表描点,用平滑的曲线将其连接即可得函数f(x)在一个周期内的图象
解答: 解:(1)∵f(x)=2sinx(sinx+cosx)-1=2sin2x+2sinxcosx-1=sin2x-cos2x=
解:(1)∵f(x)=2sinx(sinx+cosx)-1=2sin2x+2sinxcosx-1=sin2x-cos2x=
(sin2xcos
-sin
cosx)
=
sin(2x-
),
∴f(x)的最小正周期为T=
=π,
当2x-
=2kπ+
(k∈Z)时,f(x)取得最大值为
.
∴函数f(x)的最小正周期为π;最大值为
(2)列表:
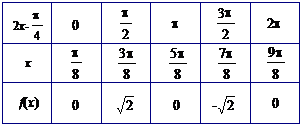
函数f(x)在一个周期内的图象如图:
 解:(1)∵f(x)=2sinx(sinx+cosx)-1=2sin2x+2sinxcosx-1=sin2x-cos2x=
解:(1)∵f(x)=2sinx(sinx+cosx)-1=2sin2x+2sinxcosx-1=sin2x-cos2x=| 2 |
| π |
| 4 |
| π |
| 4 |
=
| 2 |
| π |
| 4 |
∴f(x)的最小正周期为T=
| 2π |
| 2 |
当2x-
| π |
| 4 |
| π |
| 2 |
| 2 |
∴函数f(x)的最小正周期为π;最大值为
| 2 |
(2)列表:

函数f(x)在一个周期内的图象如图:
点评:本题考察了将三角函数式通过三角变换公式化为y=Asin(ωx+φ)的形式的技巧,三角函数的图象和性质,五点法作y=Asin(ωx+φ)型函数图象的步骤

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目