题目内容
一次函数g(x)满足g[g(x)]=9x+8,则g(x)是
- A.g(x)=9x+8
- B.g(x)=3x+8
- C.g(x)=-3x-4
- D.g(x)=3x+2或g(x)=-3x-4
D
分析:设一次函数g(x)=kx+b,利用满足g[g(x)]=9x+8,得到解决关于k,b的方程组,解方程组即可.
解答:∵一次函数g(x),
∴设g(x)=kx+b,
∴g[g(x)]=k(kx+b)+b,
又∵g[g(x)]=9x+8,
∴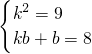 ,
,
解之得: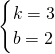 或
或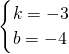 ,
,
∴g(x)=3x+2或g(x)=-3x-4.
故选D.
点评:当函数类型给定,且函数某些性质已知,我们常常可以使用待定系数法来求其解析式.可以先设出函数的一般形式,然后再利用题中条件建立方程(组)求解.
分析:设一次函数g(x)=kx+b,利用满足g[g(x)]=9x+8,得到解决关于k,b的方程组,解方程组即可.
解答:∵一次函数g(x),
∴设g(x)=kx+b,
∴g[g(x)]=k(kx+b)+b,
又∵g[g(x)]=9x+8,
∴
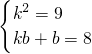 ,
,解之得:
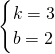 或
或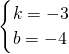 ,
,∴g(x)=3x+2或g(x)=-3x-4.
故选D.
点评:当函数类型给定,且函数某些性质已知,我们常常可以使用待定系数法来求其解析式.可以先设出函数的一般形式,然后再利用题中条件建立方程(组)求解.

练习册系列答案
相关题目
一次函数g(x)满足g[g(x)]=9x+8,则g(x)是( )
| A、g(x)=9x+8 | B、g(x)=3x+8 | C、g(x)=-3x-4 | D、g(x)=3x+2或g(x)=-3x-4 |