题目内容
(本小题14分) 已知函数f(x)=ax3+bx2+cx(a≠0)是定义在R上的奇函数,且x=-1时,函数取极值1。
(1)求a,b,c的值;
(2)若x1,x2∈[-1,1],求证:|f(x1)-f(x2)|≤2;
(3)求证:曲线y=f(x)上不存在两个不同的点A,B,使过A, B两点的切线都垂直于直线AB。
【答案】
(1)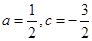 ,b=0
,b=0
(2)因为 ,那么可以运用函数单调性放缩来得到
,那么可以运用函数单调性放缩来得到 解决问题。
解决问题。
(3)对于探索性试题的分析,假设存在,然后根据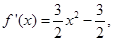 过A,B两点的切线平行,得到斜率相等,同时根据过A,B两点的切线都垂直于直线AB
过A,B两点的切线平行,得到斜率相等,同时根据过A,B两点的切线都垂直于直线AB
,则斜率之积为-1,得到方程,通过方程无解说明假设不成立,进而得到证明。
【解析】
试题分析:(1)函数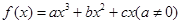 是定义在R上的奇函数,
是定义在R上的奇函数,
∴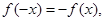 即
即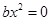 对于
对于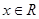 恒成立,
恒成立,
∴b=0
∴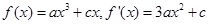
∵x=-1时,函数取极值1,∴3a+c=0,-a-c=1
解得: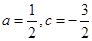
(2)
 <0,∴
<0,∴
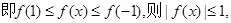
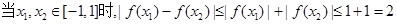
(3)设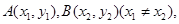
∵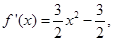 过A,B两点的切线平行,
过A,B两点的切线平行,
∴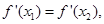 可得
可得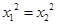
∵ ,∴
,∴ ,则
,则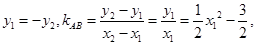
由于过A点的切线垂直于直线AB,
∴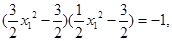
∴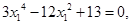 ∵△=-12<0
∵△=-12<0
∴关于x1的方程无解。
∴曲线上不存在两个不同的点A,B,过A,B两点的切线都垂直于直线AB
考点:本试题考查了导数的运用。
点评:运用导数研究函数的问题主要涉及到了函数的单调性和函数的极值以及最值问题,那么同时要熟练的掌握导数的几何意义表示切线方程。而对于不等式的恒成立问题,一般将其转换为分离参数的思想来求解不等式的成立,主要是通过最值来完成证明,属于中档题。

练习册系列答案
相关题目
 .
. ,点P为曲线
,点P为曲线 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程; 上为单调增函数,试求
上为单调增函数,试求 的取值范围.
的取值范围. 满足:
满足: ,
, ,且该函数的最小值为1.
,且该函数的最小值为1. =
=  .(其中
.(其中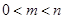 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数 ,使得函数
,使得函数
 且函数
且函数 在区间
在区间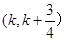 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, ……
…… .
. ,x∈[1,+∞
,x∈[1,+∞
 时,求函数f(x)的最小值
时,求函数f(x)的最小值 
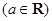 .
. ,求曲线
,求曲线 在
在 处切线的斜率;
处切线的斜率; 的单调区间;
的单调区间; ,若对任意
,若对任意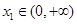 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。