题目内容
已知函数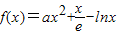 (其中a为常数,e为自然对数的底数).
(其中a为常数,e为自然对数的底数).(Ⅰ)当a=
 时,判断函数f(x)的单调性并写出其单调区间;
时,判断函数f(x)的单调性并写出其单调区间;(Ⅱ)当a>0时,求证:f(x)=0没有实数解.
【答案】分析:(Ⅰ)由条件知函数f(x)的定义域是(0,+∞),求出f(x)的导数,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,
(II)令 ,当a>0时,f(x)>
,当a>0时,f(x)> ,
, ,令h′(x)>0,可得出h(x)在(0,e)上为增函数,(e,+∞)上为减函数,从而得出h(x)最大值,最终得到即
,令h′(x)>0,可得出h(x)在(0,e)上为增函数,(e,+∞)上为减函数,从而得出h(x)最大值,最终得到即 >0恒成立,从而f(x)=0无解.或者设f (x)的极小值点为x,利用其最小值
>0恒成立,从而f(x)=0无解.或者设f (x)的极小值点为x,利用其最小值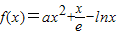 恒大于0即可证得f(x)=0没有实数解.
恒大于0即可证得f(x)=0没有实数解.
解答:解:(Ⅰ)因为x>0,
当a= 时,
时, =
= =
= ,
,
令f'(x)>0,所以 ,
,
令f'(x)<0,所以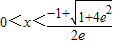 ;
;
所以函数f(x)的单调增区间为 ;
;
单调减区间为 .-------------------------------------(7分)
.-------------------------------------(7分)
(Ⅱ)解一:令
当a>0时, ----------------------------------------------------------(10分)
----------------------------------------------------------(10分)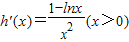
令h'(x)>0,则x∈(0,e)
所以h(x)在(0,e)上为增函数,在(e,+∞)上为减函数,
所以h(x)max=h(e)= ---------------------------------------------------------------(13分)
---------------------------------------------------------------(13分)
所以x>0时,g(x)>h(x)恒成立,即
即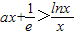 ,
,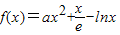 >0恒成立,
>0恒成立,
所以f (x)=0无解.----------------------------------------------------------------------(15分)
解二:设f (x)的极小值点为x,则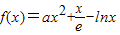 ,
,
令g(x)= ,则g'(x)=
,则g'(x)= ,---------------------------------(10分)
,---------------------------------(10分)
当x>e 时,g'(x)>0,
当x<e 时,g'(x)<0,
所以g(x)min=g(e)=0,即 >0,------------------------------------------(13分)
>0,------------------------------------------(13分)
故 >0恒成立.
>0恒成立.
所以f (x)=0无解.-------------------------------------------------(15分)
点评:本题主要考查用导数法研究函数的单调性,基本思路是:当函数为增函数时,导数大于等于零;当函数为减函数时,导数小于等于零,已知单调性求参数的范围往往转化为求相应函数的最值问题.
(II)令
 ,当a>0时,f(x)>
,当a>0时,f(x)> ,
, ,令h′(x)>0,可得出h(x)在(0,e)上为增函数,(e,+∞)上为减函数,从而得出h(x)最大值,最终得到即
,令h′(x)>0,可得出h(x)在(0,e)上为增函数,(e,+∞)上为减函数,从而得出h(x)最大值,最终得到即 >0恒成立,从而f(x)=0无解.或者设f (x)的极小值点为x,利用其最小值
>0恒成立,从而f(x)=0无解.或者设f (x)的极小值点为x,利用其最小值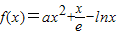 恒大于0即可证得f(x)=0没有实数解.
恒大于0即可证得f(x)=0没有实数解.解答:解:(Ⅰ)因为x>0,
当a=
 时,
时, =
= =
= ,
,令f'(x)>0,所以
 ,
,令f'(x)<0,所以
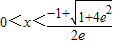 ;
;所以函数f(x)的单调增区间为
 ;
;单调减区间为
 .-------------------------------------(7分)
.-------------------------------------(7分)(Ⅱ)解一:令

当a>0时,
 ----------------------------------------------------------(10分)
----------------------------------------------------------(10分)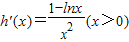
令h'(x)>0,则x∈(0,e)
所以h(x)在(0,e)上为增函数,在(e,+∞)上为减函数,
所以h(x)max=h(e)=
 ---------------------------------------------------------------(13分)
---------------------------------------------------------------(13分)所以x>0时,g(x)>h(x)恒成立,即

即
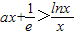 ,
,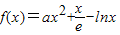 >0恒成立,
>0恒成立,所以f (x)=0无解.----------------------------------------------------------------------(15分)
解二:设f (x)的极小值点为x,则
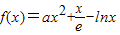 ,
,令g(x)=
 ,则g'(x)=
,则g'(x)= ,---------------------------------(10分)
,---------------------------------(10分)当x>e 时,g'(x)>0,
当x<e 时,g'(x)<0,
所以g(x)min=g(e)=0,即
 >0,------------------------------------------(13分)
>0,------------------------------------------(13分)故
 >0恒成立.
>0恒成立.所以f (x)=0无解.-------------------------------------------------(15分)
点评:本题主要考查用导数法研究函数的单调性,基本思路是:当函数为增函数时,导数大于等于零;当函数为减函数时,导数小于等于零,已知单调性求参数的范围往往转化为求相应函数的最值问题.

练习册系列答案
相关题目