Question

【题目】在平面直角坐标系中，四边形是矩形，点，点，点.以点为中心，顺时针旋转矩形，得到矩形，点的对应点分别为.

（1）如图①，当点落在边上时，求点的坐标；

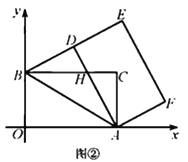
（2）如图②，当点落在线段上时，与交于点.

①求证；②求点的坐标.

（3）记为矩形对角线的交点，为的面积，求的取值范围(直接写出结果即可).

Answer 1

【答案】（1）；（2）①证明见解析；②；（3）

【解析】

（1）如图①，在中求出即可解决问题；

（2）①根据证明即可；

②设，则,构建方程求出即可解决问题；

（3）如图②中，当点在线段上时，的面积最小，当点在的延长线上时，的面积最大，求出面积的最小值以及最大值即可解决问题.

（1）如图①中

，，

，

四边形是矩形

，,

矩形是由矩形旋转得到，

（2）①

如图②中

由四边形是矩形，得到

点在线段上

由⑴可知，,又,

②如图②中，由，得到,又在矩形中，，在中

（3）如图③中

当点在线段上时，的面积最小，

最小值,

当在的延长线上时，的面积最大，

最大面积

综上所述，