题目内容
18.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的外接球的表面积为( )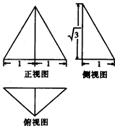
| A. | $\frac{{\sqrt{3}}}{3}π$ | B. | $\frac{16}{3}π$ | C. | $\frac{26}{3}π$ | D. | $\frac{{32\sqrt{3}}}{27}π$ |
分析 根据几何体的三视图,得出该几何体的结构特征,由此求出该几何体的外接球的半径,即可求出它的表面积.
解答  解:根据几何体的三视图知,该几何体是底面为等腰直角三角形,高为$\sqrt{3}$的直三棱锥;
解:根据几何体的三视图知,该几何体是底面为等腰直角三角形,高为$\sqrt{3}$的直三棱锥;
且该几何体的外接球球心在侧视图高上,如图所示;
设球心为O,半径为r,
则${r^2}={(\sqrt{3}-r)^2}+1$,
解得$r=\frac{{2\sqrt{3}}}{3}$,
所以,外接球的表面积为
$S=4π{r^2}=\frac{16π}{3}$.
故选:B.
点评 本题考查了几何体三视图的应用问题,也考查了球体表面积的计算问题,是基础题目.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
3.双曲线$\frac{{x}^{2}}{8-k}$+$\frac{{y}^{2}}{4-k}$=1的焦点坐标是( )
| A. | (0,±$\sqrt{12-2k}$) | B. | (±$\sqrt{12-2k}$,0) | C. | (0,±2) | D. | (±2,0) |
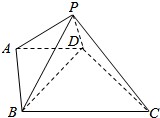 直角梯形ABCD中,∠ABC=90°,AB=AD=AP=1,BC=2,平面ABP垂直于底面ABCD.
直角梯形ABCD中,∠ABC=90°,AB=AD=AP=1,BC=2,平面ABP垂直于底面ABCD.