题目内容
若l:y=k(x-2),则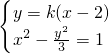 是(k2-3)x2-4k2x+4k2+3=0的
是(k2-3)x2-4k2x+4k2+3=0的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
A
分析:联立直线与双曲线的方程可以得到,(k2-3)x2-4k2x+4k2+3=0,但反之由一个方程推出直线和双曲线的方程则不能,由此判断.
解答:∵y=k(x-2),则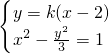 联立方程得,
联立方程得,
(k2-3)x2-4k2x+4k2+3=0,
若已知(k2-3)x2-4k2x+4k2+3=0,则不一定推出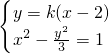 ,
,
∴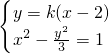 是(k2-3)x2-4k2x+4k2+3=0的充分不必要条件,
是(k2-3)x2-4k2x+4k2+3=0的充分不必要条件,
故选A.
点评:此题主要考查必要条件和充分条件的判断,此类题是高考常考的一类选择题,做题时要知道必要条件和充分条件的定义即可求解.
分析:联立直线与双曲线的方程可以得到,(k2-3)x2-4k2x+4k2+3=0,但反之由一个方程推出直线和双曲线的方程则不能,由此判断.
解答:∵y=k(x-2),则
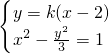 联立方程得,
联立方程得,(k2-3)x2-4k2x+4k2+3=0,
若已知(k2-3)x2-4k2x+4k2+3=0,则不一定推出
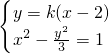 ,
,∴
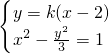 是(k2-3)x2-4k2x+4k2+3=0的充分不必要条件,
是(k2-3)x2-4k2x+4k2+3=0的充分不必要条件,故选A.
点评:此题主要考查必要条件和充分条件的判断,此类题是高考常考的一类选择题,做题时要知道必要条件和充分条件的定义即可求解.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
已知直线l:y=k(x-2)(k>0)与抛物线C:y2=8x交于A,B两点,F为抛物线C的焦点,若
=2
,则k的值是( )
| AF |
| FB |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
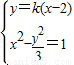 是(k2-3)x2-4k2x+4k2+3=0的( )
是(k2-3)x2-4k2x+4k2+3=0的( )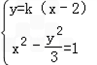 是(k2﹣3)x2﹣4k2x+4k2+3=0的
是(k2﹣3)x2﹣4k2x+4k2+3=0的