题目内容
若三角形面积和周长分别为S、L,其半径为r,则r=| 2S | L |
分析:由类比推理的规则点类比线,线类比面,面类比体,由此类比规则求解本题即可
解答:解:由已知三角形面积和周长分别为S、L,其半径为r,则r=
;三角形是平面图形,二维的,四面体是空间图形是三维的,三角形有三个边,四面体有四个面,三角形有面积,四面体有体积,则类比得:四面体体积和表面积分别为V、P,其内切球半径为R,则R=
故答案为R=
| 2S |
| L |
| 3V |
| P |
故答案为R=
| 3V |
| P |
点评:本题考查类比推理,求解的关键是熟练掌握类比的规则以及平面与空间两种图形之间类比的对应的量.如:点类比线,线类比面,面类比体,

练习册系列答案
相关题目
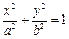
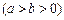 ,焦点为
,焦点为 、
、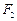 ,双曲线G:
,双曲线G: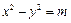
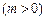 的顶点是该椭
的顶点是该椭 圆的焦点,设
圆的焦点,设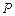 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线 、
、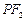 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形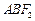 的周长等于
的周长等于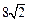 ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为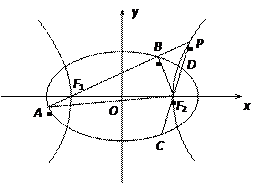
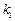 和
和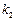 ,探求
,探求
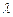 ,使得
,使得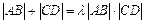 恒成立?
恒成立?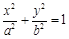
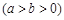 ,焦点为
,焦点为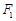 、
、 ,双曲线G:
,双曲线G: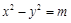
 的顶点是该椭
的顶点是该椭 圆的焦点,设
圆的焦点,设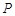 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线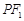 、
、 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形 的周长等于
的周长等于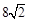 ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为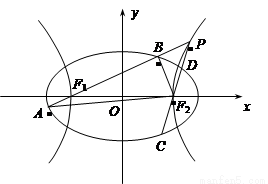
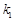 和
和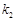 ,探求
,探求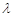 ,使得
,使得 恒成立?
恒成立?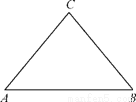
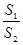 的最小值.
的最小值. (3)是否存在常数
(3)是否存在常数