Question

在直角坐标系xOy中，直线l的方程为x－y＋4＝0，曲线C的参数方程为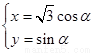 (α为参数)．

(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴)中，点P的极坐标为(4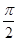，)，判断点P与直线l的位置关系；

(2)设点Q是曲线C上的一个动点，求它到直线l的距离的最小值．

 

Answer 1

【答案】

(1)点P在直线 l上．(2)最小值为.

【解析】

试题分析：(1)把极坐标系的点P(4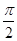，)化为直角坐标，得P(0,4)，

因为点P的直角坐标(0,4)满足直线l的方程x－y＋4＝0，所以点P在直线 l上．

(2)因为点Q在曲线C上，故可设点Q的坐标为(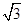cosα，sinα)，

从而点Q到直线l的距离

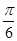＝cos(α＋)＋2，

由此得，当cos(α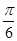＋)＝－1时，d取得最小值，且最小值为.

考点：本题主要考查极坐标与直角坐标方程的互化，点到直线的距离公式，三角函数辅助角公式，三角函数的性质。

点评：中档题，（1）利用数形结合法，极值于直角三角形边角关系，确定得到极坐标方程。（2）的解答，很好体现了参数方程的应用，将问题转化成三角函数最值的研究。