题目内容
10．已知点A（3，2），F是抛物线y2=2x的焦点，若点P在抛物线上运动，当|PA|+|PF|取最小值时，点P的坐标为（2，2）．分析 设点P在准线上的射影为D，则根据抛物线的定义可知|PF|=|PD|进而把问题转化为求|PA|+|PD|取得最小，进而可推断出当D，P，A三点共线时|PA|+|PD|最小，即可得到结论．．
解答 解：设点P在准线上的射影为D，则根据抛物线的定义可知|PF|=|PD|
∴要求|PA|+|PF|取得最小值，即求|PA|+|PD|取得最小
当D，P，A三点共线时|PA|+|PD|最小，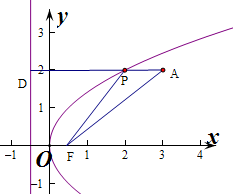
∵A（3，2），∴P点的纵坐标y=2，
此时由y2=2x得x=$\frac{{2}^{2}}{2}=2$，
即P（2，2），
故答案为：（2，2）
点评 本题主要考查了抛物线的应用．考查了学生数形结合的思想和抛物线定义的应用，利用抛物线的定义是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．如果函数y=3sin（2x+φ）的图象关于直线x=$\frac{π}{6}$对称，则|φ|的最小值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
5．抛物线y2=2px上横坐标为6的点到此抛物线焦点的距离为10，则该抛物线的焦点到准线的距离为（ ）
| A． | 4 | B． | 8 | C． | 16 | D． | 32 |
定义：f1（x）=f（x），当n≥2且n∈N*时，fn（x）=f（fn-1（x）），对于函数f（x）定义域内的x0，若存在正整数n是使得fn（x0）=x0成立的最小正整数，则称n是点x0的最小正周期，x0称为f（x）的n-周期点．已知定义在[0，1]上的函数f（x）的图象如图，对于函数f（x），下列说法正确的是②③⑤（写出你认为正确的所有命题的序号）