题目内容
已知双曲线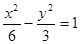 的焦点为F1、F2,点M在双曲线上,且MF1
的焦点为F1、F2,点M在双曲线上,且MF1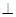 x轴,则F1到直线F2M的距离为 ( )
x轴,则F1到直线F2M的距离为 ( )
A.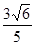 ;
B.
;
B.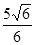 ; C.
; C.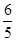 ; D.
; D.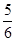
【答案】
C
【解析】
MF1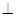 x轴,
x轴,
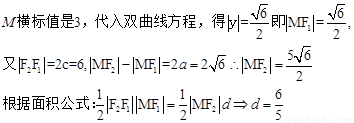

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
已知双曲线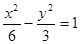 的焦点为F1、F2,点M在双曲线上,且MF1
的焦点为F1、F2,点M在双曲线上,且MF1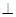 x轴,则F1到直线F2M的距离为 ( )
x轴,则F1到直线F2M的距离为 ( )
A.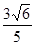 ;
B.
;
B.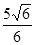 ; C.
; C.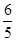 ; D.
; D.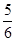
C
【解析】
MF1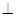 x轴,
x轴,

 名校课堂系列答案
名校课堂系列答案