题目内容
已知抛物线 的焦点为F,准线为l,是否存在双曲线C,同时满足以下两个条件:
的焦点为F,准线为l,是否存在双曲线C,同时满足以下两个条件:
(Ⅰ)双曲线C的一个焦点为F,相应于F的准线为l;
(Ⅱ)双曲线C截与直线x-y=0垂直的直线所得线段AB的长为2 ,并且线段AB的中点恰好在直线x-y=0上.
,并且线段AB的中点恰好在直线x-y=0上.
若存在,求出该双曲线C的方程;若不存在,说明理由.
答案:
解析:
解析:
|
本小题主要考查直线与圆锥曲线的有关知识,以及综合运用数学知识解决问题的能力. 解:假设满足题意的双曲线C存在,并设其离心率为e,AB的中点坐标为(a,a),点A的坐标为 ∵直线AB的斜率 ∴ 由此解得 不失一般性,取A(a-1,a+1),B(a+1,a-1). 由于F(0,0)和l:x=-1是对应的焦点和准线, 解之,得a=-1,e=2. 故满足题意的双曲线存在,其方程为 |

练习册系列答案
相关题目
已知抛物线的焦点坐标是F(0,-2),则它的标准方程为( )
| A、x2=-8y | B、x2=3y | C、y2=-3x | D、y2=3x |
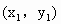 ,则点B的坐标为(2a-
,则点B的坐标为(2a- ,2a-
,2a-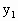 ).
).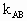 =-1,且|AB|=
=-1,且|AB|=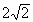
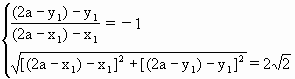

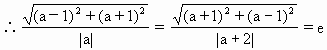
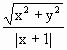 =2,即
=2,即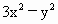 +8x+4=0.
+8x+4=0.