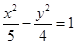题目内容
已知双曲线的中心为原点,F(3,0)是双曲线的-个焦点,
x-2y=0是双曲线的一条渐近线,则双曲线的标准方程为( )
| 5 |
分析:根据已知条件,利用双曲线的焦点坐标,设出双曲线的标准方程,再由双曲线的渐近线方程,求出双曲线的标准方程.
解答:解:∵双曲线的中心为原点,F(3,0)是双曲线的-个焦点,
∴设双曲线方程为
-
=1,a>0,
∵
x-2y=0是双曲线的一条渐近线,
∴
=
,解得a2=4,
∴双曲线方程为
-
=1.
故选D.
∴设双曲线方程为
| x2 |
| a2 |
| y2 |
| 9-a2 |
∵
| 5 |
∴
| ||
| a |
| ||
| 2 |
∴双曲线方程为
| x2 |
| 4 |
| y2 |
| 5 |
故选D.
点评:本题考查双曲线的标准方程的求法,解题时要认真审题,熟练掌握双曲线的简单性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的中心为原点,
的中心为原点, 是
是 的直线
的直线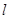 与
与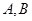 两点,且
两点,且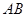 的中点为
的中点为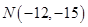 ,则
,则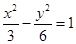 B.
B.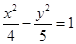 C.
C.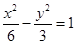 D.
D.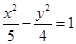
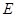 的中心为原点,
的中心为原点,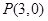 是
是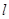 与
与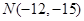 ,则
,则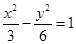 B.
B.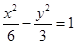
 D.
D.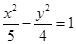
 的中心为原点,
的中心为原点,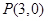 是
是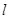 与
与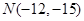 ,则
,则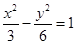 B.
B.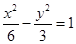 C.
C.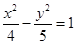 D.
D.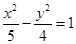
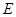 的中心为原点,
的中心为原点,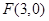 是
是 与
与 ,则
,则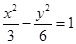 B.
B. 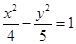 C.
C.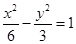 D.
D.