题目内容
【题目】△ABC中,角A,B,C的对边分别为a,b,c,且三角形的面积S= ![]() accosB.
accosB.
(1)求角B的大小;
(2)若a=2 ![]() ,点D在AB的延长线上,且AD=3,cos∠ADC=
,点D在AB的延长线上,且AD=3,cos∠ADC= ![]() ,求b的值.
,求b的值.
【答案】
(1)解:∵S= ![]() accosB=
accosB= ![]() acsinB,
acsinB,
∴tanB= ![]() ,
,
∴B= ![]() .
.
(2)解:如图,
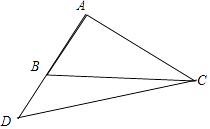
∵B= ![]() .∴∠CBD=
.∴∠CBD= ![]() ,
,
∵cos∠ADC= ![]() ,∴sin∠ADC=
,∴sin∠ADC= ![]() =
= ![]() ,
,
∴在△BCD中,由正弦定理 ![]() ,可得:
,可得: ![]() ,解得:CD=9,
,解得:CD=9,
∴在△ADC中,由余弦定理可得:b2=AD2+CD2﹣2ADCDcos∠ADC=9+81﹣2× ![]() =54.
=54.
∴b=3 ![]() .
.
【解析】(1)由已知利用三角形面积公式,同角三角函数基本关系式可求tanB= ![]() ,由特殊角的三角函数值即可得解B的值.(2)由已知可求∠CBD=
,由特殊角的三角函数值即可得解B的值.(2)由已知可求∠CBD= ![]() ,sin∠ADC=
,sin∠ADC= ![]() ,由正弦定理解得CD,进而在△ADC中,由余弦定理可得b的值.
,由正弦定理解得CD,进而在△ADC中,由余弦定理可得b的值.
【考点精析】根据题目的已知条件,利用正弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目