题目内容
已知函数f(x)=cos(2x+ )+
)+ -
- +
+ sinx·cosx
sinx·cosx
⑴ 求函数f(x)的单调减区间; ⑵ 若xÎ[0, ],求f(x)的最值;
],求f(x)的最值;
⑶ 若f(a)= ,2a是第一象限角,求sin2a的值.
,2a是第一象限角,求sin2a的值.
 )+
)+ -
- +
+ sinx·cosx
sinx·cosx⑴ 求函数f(x)的单调减区间; ⑵ 若xÎ[0,
 ],求f(x)的最值;
],求f(x)的最值;⑶ 若f(a)=
 ,2a是第一象限角,求sin2a的值.
,2a是第一象限角,求sin2a的值.⑴ ⑴f(x)的减区间是[ +kp,
+kp,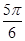 +kp](kÎZ) ⑵x=
+kp](kÎZ) ⑵x= 时,f(x)max=1
时,f(x)max=1
⑶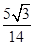
 +kp,
+kp,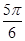 +kp](kÎZ) ⑵x=
+kp](kÎZ) ⑵x= 时,f(x)max=1
时,f(x)max=1 ⑶
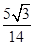
第一问中,利用f(x)=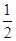 cos2x-
cos2x-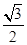 sin2x-cos2x+
sin2x-cos2x+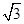 sin2x=
sin2x=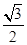 sin2x-
sin2x-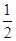 cos2x=sin(2x-
cos2x=sin(2x- )令
)令 +2kp≤2x-
+2kp≤2x- ≤
≤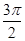 +2kp,
+2kp,
解得 +kp≤x≤
+kp≤x≤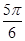 +kp
+kp
第二问中,∵xÎ[0, ],∴2x-
],∴2x- Î[-
Î[- ,
,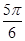 ],
],
∴当2x- =-
=- ,即x=0时,f(x)min=-
,即x=0时,f(x)min=-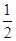 ,
,
当2x- =
= , 即x=
, 即x= 时,f(x)max=1
时,f(x)max=1
第三问中,(a)=sin(2a- )=
)= ,2a是第一象限角,即2kp<2a<
,2a是第一象限角,即2kp<2a< +2kp
+2kp
∴ 2kp- <2a-
<2a- <
< +2kp,∴ cos(2a-
+2kp,∴ cos(2a- )=
)=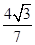
利用构造角得到sin2a=sin[(2a- )+
)+ ]
]
解:⑴ f(x)=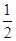 cos2x-
cos2x-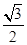 sin2x-cos2x+
sin2x-cos2x+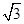 sin2x ………2分
sin2x ………2分
=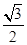 sin2x-
sin2x-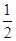 cos2x=sin(2x-
cos2x=sin(2x- ) ……………………3分
) ……………………3分
⑴ 令 +2kp≤2x-
+2kp≤2x- ≤
≤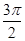 +2kp,
+2kp,
解得 +kp≤x≤
+kp≤x≤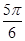 +kp ……………………5分
+kp ……………………5分
∴ f(x)的减区间是[ +kp,
+kp,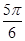 +kp](kÎZ) ……………………6分
+kp](kÎZ) ……………………6分
⑵ ∵xÎ[0, ],∴2x-
],∴2x- Î[-
Î[- ,
,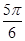 ], ……………………7分
], ……………………7分
∴当2x- =-
=- ,即x=0时,f(x)min=-
,即x=0时,f(x)min=-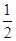 , ……………………8分
, ……………………8分
当2x- =
= , 即x=
, 即x= 时,f(x)max=1 ……………………9分
时,f(x)max=1 ……………………9分
⑶ f(a)=sin(2a- )=
)= ,2a是第一象限角,即2kp<2a<
,2a是第一象限角,即2kp<2a< +2kp
+2kp
∴ 2kp- <2a-
<2a- <
< +2kp,∴ cos(2a-
+2kp,∴ cos(2a- )=
)=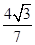 , ……………………11分
, ……………………11分
∴ sin2a=sin[(2a- )+
)+ ]
]
=sin(2a- )·cos
)·cos +cos(2a-
+cos(2a- )·sin
)·sin ………12分
………12分
= ×
×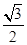 +
+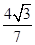 ×
×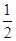 =
=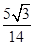
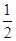 cos2x-
cos2x-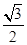 sin2x-cos2x+
sin2x-cos2x+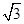 sin2x=
sin2x=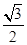 sin2x-
sin2x-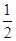 cos2x=sin(2x-
cos2x=sin(2x- )令
)令 +2kp≤2x-
+2kp≤2x- ≤
≤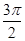 +2kp,
+2kp,解得
 +kp≤x≤
+kp≤x≤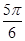 +kp
+kp 第二问中,∵xÎ[0,
 ],∴2x-
],∴2x- Î[-
Î[- ,
,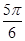 ],
],∴当2x-
 =-
=- ,即x=0时,f(x)min=-
,即x=0时,f(x)min=-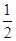 ,
,当2x-
 =
= , 即x=
, 即x= 时,f(x)max=1
时,f(x)max=1第三问中,(a)=sin(2a-
 )=
)= ,2a是第一象限角,即2kp<2a<
,2a是第一象限角,即2kp<2a< +2kp
+2kp∴ 2kp-
 <2a-
<2a- <
< +2kp,∴ cos(2a-
+2kp,∴ cos(2a- )=
)=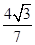
利用构造角得到sin2a=sin[(2a-
 )+
)+ ]
]解:⑴ f(x)=
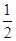 cos2x-
cos2x-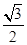 sin2x-cos2x+
sin2x-cos2x+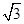 sin2x ………2分
sin2x ………2分=
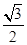 sin2x-
sin2x-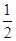 cos2x=sin(2x-
cos2x=sin(2x- ) ……………………3分
) ……………………3分⑴ 令
 +2kp≤2x-
+2kp≤2x- ≤
≤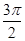 +2kp,
+2kp,解得
 +kp≤x≤
+kp≤x≤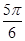 +kp ……………………5分
+kp ……………………5分∴ f(x)的减区间是[
 +kp,
+kp,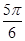 +kp](kÎZ) ……………………6分
+kp](kÎZ) ……………………6分⑵ ∵xÎ[0,
 ],∴2x-
],∴2x- Î[-
Î[- ,
,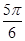 ], ……………………7分
], ……………………7分∴当2x-
 =-
=- ,即x=0时,f(x)min=-
,即x=0时,f(x)min=-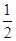 , ……………………8分
, ……………………8分当2x-
 =
= , 即x=
, 即x= 时,f(x)max=1 ……………………9分
时,f(x)max=1 ……………………9分⑶ f(a)=sin(2a-
 )=
)= ,2a是第一象限角,即2kp<2a<
,2a是第一象限角,即2kp<2a< +2kp
+2kp∴ 2kp-
 <2a-
<2a- <
< +2kp,∴ cos(2a-
+2kp,∴ cos(2a- )=
)=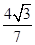 , ……………………11分
, ……………………11分∴ sin2a=sin[(2a-
 )+
)+ ]
]=sin(2a-
 )·cos
)·cos +cos(2a-
+cos(2a- )·sin
)·sin ………12分
………12分=
 ×
×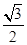 +
+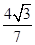 ×
×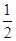 =
=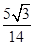

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 且
且 ,函数
,函数
 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; ,分别求
,分别求 及
及 的值
的值 上的一个最高点的坐标为
上的一个最高点的坐标为 ,则此点到相邻最低点间的曲线与
,则此点到相邻最低点间的曲线与 轴交于点(
轴交于点( ),若
),若 .
.
 上的图像.
上的图像.
 ,
, .
. 时,求函数
时,求函数
 的一条对称轴为( )
的一条对称轴为( )



 ,
, ,则
,则 是( )
是( ) 的奇函数
的奇函数 的奇函数
的奇函数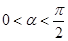 ,
, ,则
,则 ( ▲ )
( ▲ ) 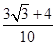
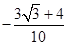
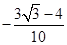
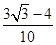
 ,若
,若 ,则
,则 的取值范围是 。
的取值范围是 。