题目内容
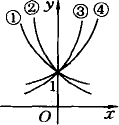
 如图是指数函数①y=ax、②y=bx、③y=cx、④y=dx的图象,则a,b,c,d与1的大小关系是( )
如图是指数函数①y=ax、②y=bx、③y=cx、④y=dx的图象,则a,b,c,d与1的大小关系是( )分析:有指数函数的单调性分析得到a,b大于1,c,d大于0小于1,再通过取x=1得到具体的大小关系.
解答:解:∵当底数大于1时指数函数是定义域内的增函数,当底数大于0小于1时是定义域内的减函数,
可知a,b大于1,c,d大于0小于1.
又由图可知a1>b1,即a>b.d1<c1,即d<c.
∴a,b,c,d与1的大小关系是d<c<1<b<a.
故选:B.
可知a,b大于1,c,d大于0小于1.
又由图可知a1>b1,即a>b.d1<c1,即d<c.
∴a,b,c,d与1的大小关系是d<c<1<b<a.
故选:B.
点评:本题考查了指数函数的图象和性质,考查了指数函数的单调性,训练了特值思想方法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图的曲线是指数函数y=ax的图象,已知a的值取
如图的曲线是指数函数y=ax的图象,已知a的值取