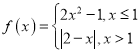题目内容
【题目】已知关于x的一元二次不等式ax2+2x+b>0的解集为{x|x≠c},则![]() (其中a+c≠0)的取值范围为_____.
(其中a+c≠0)的取值范围为_____.
【答案】(﹣∞,﹣6]∪[6,+∞)
【解析】
由条件利用二次函数的性质可得ac=﹣1,ab=1, 即c=-b将![]() 转为(a﹣b)+
转为(a﹣b)+![]() ,利用基本不等式求得它的范围.
,利用基本不等式求得它的范围.
因为一元二次不等式ax2+2x+b>0的解集为{x|x≠c},由二次函数图像的性质可得a>0,二次函数的对称轴为x=![]() =c,△=4﹣4ab=0,
=c,△=4﹣4ab=0,
∴ac=﹣1,ab=1,∴c=![]() ,b=
,b=![]() ,即c=-b,
,即c=-b,
则![]() =
=![]() =(a﹣b)+
=(a﹣b)+![]() ,
,
当a﹣b>0时,由基本不等式求得(a﹣b)+![]() ≥6,
≥6,
当a﹣b<0时,由基本不等式求得﹣(a﹣b)﹣![]() ≥6,即(a﹣b)+
≥6,即(a﹣b)+![]() ≤﹣6,
≤﹣6,
故![]() (其中a+c≠0)的取值范围为:(﹣∞,﹣6]∪[6,+∞),
(其中a+c≠0)的取值范围为:(﹣∞,﹣6]∪[6,+∞),
故答案为:(﹣∞,﹣6]∪[6,+∞).

练习册系列答案
相关题目