题目内容
设Sn,Tn分别为下列表格中的两个等差数列{an},{bn}的前n项和.
n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
an | 5 | 3 | 1 | -1 | -3 | -5 | -7 | … |
bn | -14 | -10 | -6 | -2 | 2 | 6 | 10 | … |
(1)请求出S1,S2,S4,S5和T2,T3,T5,T6;
(2)根据上述结果,对于存在正整数k满足ak+ak+1=0的等差数列{an}的前n项和Sn(n≤2k-1)的规律,猜想一个正确的结论,并加以证明.
解:(1)数列{an}中,a1=5,公差d=-2.
∴Sn=na1+![]() d=5n+
d=5n+![]() ×(-2)=-n2+6n,
×(-2)=-n2+6n,
∴S1=5,S2=8,S4=8,S5=5.
数列{bn}中,b1=-14,d′=4.∴Tn=-14n+![]() ×4=2n2-16n,
×4=2n2-16n,
∴T2=-24,T3=-30,T5=-30,T6=-24.
(2)若ak+ak+1=0,则Sk+n=Sk-n(或Sn=S2k-n)(n≤2k-1,k>n).
证明如下:∵{an}是等差数列,
∴Sk-n-Sk+n=(k-n)a1+![]() d-(k+n)a1
d-(k+n)a1![]()
=-2na1+![]() [(k-n)2-k+n-(k+n)2+k+n]
[(k-n)2-k+n-(k+n)2+k+n]
=-2na1+![]() (k2-2kn+n2+n-k2-2kn-n2+n)
(k2-2kn+n2+n-k2-2kn-n2+n)
=-2na1+![]() (-4kn+2n)=-2na1+dn(1-2k).
(-4kn+2n)=-2na1+dn(1-2k).
又∵ak+ak+1=0,∴a1+(k-1)d+a1+kd=0,d=![]() ,
,
∴Sk-n-Sk+n=-2na1+![]() (1-2k)=0,即Sk-n=Sk+n.
(1-2k)=0,即Sk-n=Sk+n.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
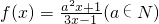 ,方程f(x)=-2x+7有两个根x1,x2,且x1<1<x2<3.
,方程f(x)=-2x+7有两个根x1,x2,且x1<1<x2<3.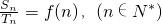 ,设
,设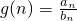 ,求g(n)的解析式及g(n)的最大值;
,求g(n)的解析式及g(n)的最大值; ,方程f(x)=-2x+7有两个根x1,x2,且x1<1<x2<3.
,方程f(x)=-2x+7有两个根x1,x2,且x1<1<x2<3. ,设
,设 ,求g(n)的解析式及g(n)的最大值;
,求g(n)的解析式及g(n)的最大值;