题目内容
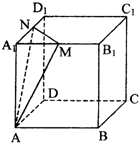
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是棱A1B1、A1D1的中点,则点B到平面AMN的距离是
.
| 2 |
| 3 |
| 2 |
| 3 |

分析:连接AC、BD交于点O,连接A1C1与MN的交点为E,连接AE、B1D1,作OH⊥AE于H.然后利用三角形的中位线定理和平行四边形对边平行,证明出MN∥BD,结合线平行的判定定理,得到BD∥平面AMN,所以点B到平面AMN的距离,即为直线BD到平面AMN的距离.接下来利用直线与平面垂直的判定定理,证明出OH⊥平面AMN,得OH即为直线BD到平面AMN的距离.这样就证出了OH即是点B到平面AMN的距离,最后利用Rt△A1EA∽Rt△HAO,可以求出OH的长,求出点B到平面AMN的距离.
解答:解:连接AC、BD交于点O,连接A1C1与MN的交点为E,
连接AE、B1D1,作OH⊥AE于H,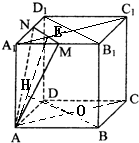
可得OH即是点B到平面AMN的距离.下面进行证明
∵△A1B1D1中,M、N分别是棱A1B1、A1D1的中点,
∴MN∥B1D1
∵B1D1∥BD
∴MN∥BD
∵MN⊆平面AMN,BD?平面AMN
∴BD∥平面AMN
点B到平面AMN的距离,即为直线BD到平面AMN的距离
∵AA1⊥平面ABCD,BD⊆平面ABCD
∴BD⊥AA1
又∵BD⊥AC,AC∩A1A=A,AC、A1A⊆平面AA1C1C
∴BD⊥平面AA1C1C
∵MN∥BD
∴MN⊥平面AA1C1C
∵OH⊆平面AA1C1C
∴OH⊥MN
又∵OH⊥AE,MN∩AE=E,MN、AE⊆平面AMN
∴OH⊥平面AMN
OH即为直线BD到平面AMN的距离
∴OH即是点B到平面AMN的距离.
∵在正方形A1B1C1D1中,边长为1,
M、N分别是A1B1、A1D1的中点
∴A1E=
A1C1=
∴Rt△A1AE中,AE=
=
=
在Rt△HAO中,AO=
AC=
∵∠HAO=∠A1EA=90°-∠A1AE
∴Rt△A1EA∽Rt△HAO
∴
=
⇒OH=
=
故答案为:
连接AE、B1D1,作OH⊥AE于H,

可得OH即是点B到平面AMN的距离.下面进行证明
∵△A1B1D1中,M、N分别是棱A1B1、A1D1的中点,
∴MN∥B1D1
∵B1D1∥BD
∴MN∥BD
∵MN⊆平面AMN,BD?平面AMN
∴BD∥平面AMN
点B到平面AMN的距离,即为直线BD到平面AMN的距离
∵AA1⊥平面ABCD,BD⊆平面ABCD
∴BD⊥AA1
又∵BD⊥AC,AC∩A1A=A,AC、A1A⊆平面AA1C1C
∴BD⊥平面AA1C1C
∵MN∥BD
∴MN⊥平面AA1C1C
∵OH⊆平面AA1C1C
∴OH⊥MN
又∵OH⊥AE,MN∩AE=E,MN、AE⊆平面AMN
∴OH⊥平面AMN
OH即为直线BD到平面AMN的距离
∴OH即是点B到平面AMN的距离.
∵在正方形A1B1C1D1中,边长为1,
M、N分别是A1B1、A1D1的中点
∴A1E=
| 1 |
| 4 |
| ||
| 4 |
∴Rt△A1AE中,AE=
| A 1A 2+A1E2 |
12+(
|
| 3 |
| 4 |
| 2 |
在Rt△HAO中,AO=
| 1 |
| 2 |
| ||
| 2 |
∵∠HAO=∠A1EA=90°-∠A1AE
∴Rt△A1EA∽Rt△HAO
∴
| AA 1 |
| OH |
| AE |
| AO |
| AA 1•AO |
| AE |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题综合考查了直线与平面平行的判定、直线与平面垂直的判定,以及空间点、线、面间的距离计算等知识点,考查了空间想象力,属于中档题.

练习册系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
