题目内容
已知A(2,0,0),B(0,1,0),C(0,0,2),则P(2,1,4)到平面ABC的距离是 .
分析:利用已知条件求出
,
,
,利用向量垂直求出平面ABC的法向量,通过向量数量积求出P(2,1,4)到平面ABC的距离.
| AB |
| AC |
| AP |
解答:解:
=(-2,1,0),
=(-2,0,2),
=(0,1,4).
设平面ABC的法向量为
=(x,y,z),
则由
•
=0,
•
=0
得:
,解得x=z,y=2x
令z=1,则
=(1,2,1)
所以点P到平面平面ABC的距离是d=
=
=
.
故答案为:
.
| AB |
| AC |
| AP |
设平面ABC的法向量为
| n |
则由
| n |
| AB |
| n |
| AC |
得:
|
令z=1,则
| n |
所以点P到平面平面ABC的距离是d=
| ||||
|
|
| 0+2+4 | ||
|
| 6 |
故答案为:
| 6 |
点评:本题考查空间向量的数量积的运算,平面法向量的求法,点到平面的距离的求法,考查计算能力.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
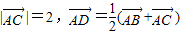 .
. ,且直线l与点D的轨迹相切,求该椭圆的方程;
,且直线l与点D的轨迹相切,求该椭圆的方程;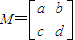 对应变换的作用下,得到的对应点分别为A'(0,0),
对应变换的作用下,得到的对应点分别为A'(0,0),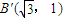 ,C'(0,2),求矩阵M.
,C'(0,2),求矩阵M. -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0, (x>0),
(x>0), ,又a<0,
,又a<0,