Question

6．如图，在多面体ABC-A₁B₁C₁中，侧面AA₁B₁B⊥底面A₁B₁C₁，四边形AA₁B₁B是矩形，A₁C₁=A₁B₁，∠B₁A₁C₁=120°，BC∥B₁C₁，B₁C₁=2BC．
（1）求证：A₁C⊥B₁C₁；
（2）当二面角C-AC₁-B₁的正切值为2时，求$\frac{A{A}_{1}}{{A}_{1}{B}_{1}}$的值．

Answer 1

分析 （1）由题意，取B₁C₁的中点为M，连接CM，可先证B₁C₁⊥面A₁MC，再由线在垂直定义证出A₁C⊥B₁C₁；
（2）二面角C-AC₁-B₁的正切值为2，可得出二面角的余弦值为$\frac{1}{\sqrt{5}}$，建立空间坐标系，设AA₁=1，A₁B₁=a，以a表示出两个平面的法向量，由公式将二面角的余弦值用a表示出，代入cosθ=$\frac{1}{\sqrt{5}}$，从此方程中求出a，即可得出所求．

解答 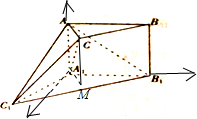解：（1）证：由题意，取B₁C₁的中点为M，连接CM，由于B₁C₁=2BC，BC∥B₁C₁，可得出BC∥B₁M，且BC=B₁M，所以?BCMB₁，
 又在多面体ABC-A₁B₁C₁中，侧面AA₁B₁B⊥底面A₁B₁C₁，四边形AA₁B₁B是矩形，
∴B₁B⊥面A₁B₁C₁，又B₁M?面A₁B₁C₁，
∴B₁B⊥B₁M，即?BCMB₁是矩形，所以CM⊥B₁M，即可得CM⊥B₁C₁，
连接C₁M，由于A₁C₁=A₁B₁，M是中点，故A₁M⊥B₁C₁，由线面垂直的判定定理可以得出B₁C₁⊥面A₁MC，
又A₁C?面A₁MC，故可得A₁C⊥B₁C₁；
（2）设A₁B₁=1，AA₁=a，平面AB₁C₁的一个法向量为$\overrightarrow{m}$=（x，y，z），∴$\overrightarrow{m}$⊥$\overrightarrow{{C}_{1}A}$，$\overrightarrow{m}$⊥$\overrightarrow{{B}_{1}{C}_{1}}$，
∵$\overrightarrow{{B}_{1}A}$=（0，-1，a），$\overrightarrow{{B}_{1}{C}_{1}}$=（$\frac{\sqrt{3}}{2}$，-$\frac{3}{2}$，0），则$\left\{\begin{array}{l}{x-\sqrt{3}y=0}\\{y-az=0}\end{array}\right.$，取$\overrightarrow{m}$=（$\sqrt{3}$，1，$\frac{1}{a}$），
设平面AC₁C的一个法向量为$\overrightarrow{n}$=（x，y，z），所以$\overrightarrow{n}$⊥$\overrightarrow{{C}_{1}A}$，$\overrightarrow{n}$⊥$\overrightarrow{CA}$，
∵$\overrightarrow{{C}_{1}A}$=（-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$，a），$\overrightarrow{AC}$=（$\frac{\sqrt{3}}{4}$，$\frac{1}{4}$，0），则$\left\{\begin{array}{l}{\sqrt{3}x+y=0}\\{\sqrt{3}x-y-2az=0}\end{array}\right.$，取$\overrightarrow{n}$=（1，-$\sqrt{3}$，$\frac{\sqrt{3}}{a}$），
∵二面角C-AC₁-B₁的正切值为2，∴二面角C-AC₁-B₁的余弦值为$\frac{\sqrt{5}}{5}$，即|cos＜$\overrightarrow{m}$，$\overrightarrow{n}$＞|=$\frac{\sqrt{5}}{5}$，
∴$\frac{\frac{\sqrt{3}}{{a}^{2}}}{\sqrt{（4+\frac{3}{{a}^{2}}）（4+\frac{1}{{a}^{2}}）}}$=$\frac{\sqrt{5}}{5}$，
解得：a=$\frac{\sqrt{2}}{2}$，
∴$\frac{A{A}_{1}}{{A}_{1}{B}_{1}}$=$\frac{\sqrt{2}}{2}$

点评 本题考查二面角的求法与线线垂直的证明，本题第一小题，线线垂直通常用线面垂直来证，第二题中由于此二面角平面角不易做，宜采用空间向量法表示出二面角，空间向量求二面角是高考中的高频考点，题后要注意总结此方法的原理与解答过程，争取熟练掌握．