题目内容
1．已知F1（-$\sqrt{2}$，0）、F2（$\sqrt{2}$，0）为椭圆的焦点，A为其上顶点，∠F1AF2=90°，则圆的离心率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{2}$ | D． | $\frac{\sqrt{2}}{4}$ |
分析 利用已知条件求出b、c关系，然后求解椭圆的离心率即可．
解答 解：F1（-$\sqrt{2}$，0）、F2（$\sqrt{2}$，0）为椭圆的焦点，A为其上顶点，∠F1AF2=90°，
由椭圆的对称性可知：b=c=$\sqrt{2}$，
可得a=$\sqrt{{b}^{2}+{c}^{2}}$=2．
椭圆的离心率为：e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$．
故选：B．
点评 本题考查椭圆离心率的求法，考查计算能力．
练习册系列答案
相关题目
12．已知f（x）是定义在实数集R上的可导函数，且其导函数为f′（x），若f′（x）＜f（x）在R上恒成立，则不等式ef（x）＞f（1）ex上的解集为（ ）
| A． | （1，+∞） | B． | （-∞，1） | C． | （-1，1） | D． | （-∞，1）∪（1，+∞） |
9．已知$f（x+\frac{1}{x}）={x^2}+\frac{1}{x^2}$，则函数f（x）=（ ）
| A． | x2-2（x≠0） | B． | x2-2（x≥2） | C． | x2-2（|x|≥2） | D． | x2-2 |
6．
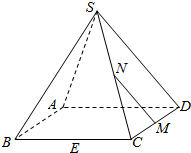如图，在正四棱锥S-ABCD中，E，M，N分别是B，CD，SC的中点，P在线段MN上且NP=2PM，下列四个结论：
①EP⊥AC；②EP⊥面SAC；③EP∥BD；④EP∥面SBD中成立的为（ ）
如图，在正四棱锥S-ABCD中，E，M，N分别是B，CD，SC的中点，P在线段MN上且NP=2PM，下列四个结论：①EP⊥AC；②EP⊥面SAC；③EP∥BD；④EP∥面SBD中成立的为（ ）
| A． | ①③ | B． | ①② | C． | ①④ | D． | ②④ |
10．若函数f（x）=$\frac{x+b}{（2x+1）（x-a）}$为奇函数，则a+b=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | 1 |
11．已知A（1，-1），B（4，2），P为AB的中点，则$\overrightarrow{AP}$的坐标为（ ）
| A． | （$\frac{3}{2}$，$\frac{3}{2}$） | B． | （$\frac{3}{2}$，-$\frac{1}{2}$） | C． | （5，4） | D． | （3，-3） |