题目内容
把一个圆锥截成圆台,已知圆台的上、下底面半径之比为1:2,母线长为6cm,则圆锥的母线长为
12
12
cm.分析:作出圆锥和圆台的轴截面,利用圆台的上、下底面半径之比为1:2,母线长为6cm,建立方程关系,可求圆锥的母线长.
方法1:使用相似三角形的性质,建立等式关系.
方法2:利用中点的性质,建立等式关系,进行求解即可.
方法1:使用相似三角形的性质,建立等式关系.
方法2:利用中点的性质,建立等式关系,进行求解即可.
解答:解:方法1:
作出圆锥和圆台的轴截面如图: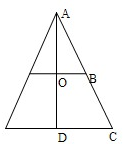
由题意设圆台的上底半径OB=x,下底半径DC=2x,母线BC=6cm,
则根据三角形的相似性可知,
=
,
即
=
=
,
解得AC=12.
方法2:
∵圆台的上、下底面半径之比为1:2,
∴B为AC的中点,
∴AB=BC=6,
∴AC=6+6=12(cm),
故答案为:12cm.
作出圆锥和圆台的轴截面如图:

由题意设圆台的上底半径OB=x,下底半径DC=2x,母线BC=6cm,
则根据三角形的相似性可知,
| OB |
| DC |
| AB |
| AC |
即
| x |
| 2x |
| AC-BC |
| AC |
| AC-6 |
| AC |
解得AC=12.
方法2:
∵圆台的上、下底面半径之比为1:2,
∴B为AC的中点,
∴AB=BC=6,
∴AC=6+6=12(cm),
故答案为:12cm.
点评:本题主要考查圆锥和圆台的结构,利用轴截面法是解决本题的关键,比较基础.

练习册系列答案
相关题目
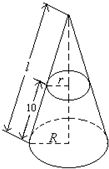 把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:4,母线长10cm.求:圆锥的母线长.
把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:4,母线长10cm.求:圆锥的母线长.