题目内容
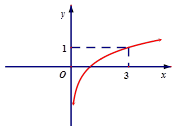
已知函数f(x)=
下列是关于函数y=f[f(x)]+1的零点个数的4个判断:
①当k>0时,有3个零点;
②当k<0时,有2个零点;
③当k>0时,有4个零点;
④当k<0时,有1个零点.
则正确的判断是( )
|
①当k>0时,有3个零点;
②当k<0时,有2个零点;
③当k>0时,有4个零点;
④当k<0时,有1个零点.
则正确的判断是( )
| A.①④ | B.②③ | C.①② | D.③④ |
由y=f[f(x)]+1=0得f[f(x)]+1=0,即f[f(x)]=-1,
设f(x)=t,则方程f[f(x)]=-1等价为f(t)=-1,
①若k>0,作出函数f(x)的图象如图: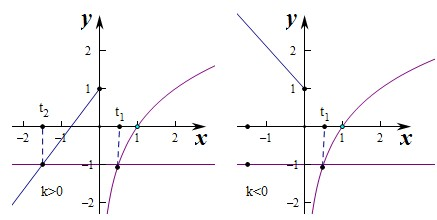
∵f(t)=-1,
∴此时方程f(t)=-1有两个根其中t2<0,0<t1<1,
由f(x)=t2,<0,知此时x有两解,
由f(x)=t1∈(0,1)知此时x有两解,
此时共有4个解,即函数y=f[f(x)]+1有4个零点.
②若k<0,作出函数f(x)的图象如图:
∵f(t)=-1,
∴此时方程f(t)=-1有一个根t1,其中0<t1<1,
由f(x)=t1∈(0,1)知此时x只有1个解,
即函数y=f[f(x)]+1有1个零点.
综上:只有③④正确,
故选:D.
设f(x)=t,则方程f[f(x)]=-1等价为f(t)=-1,
①若k>0,作出函数f(x)的图象如图:

∵f(t)=-1,
∴此时方程f(t)=-1有两个根其中t2<0,0<t1<1,
由f(x)=t2,<0,知此时x有两解,
由f(x)=t1∈(0,1)知此时x有两解,
此时共有4个解,即函数y=f[f(x)]+1有4个零点.
②若k<0,作出函数f(x)的图象如图:
∵f(t)=-1,
∴此时方程f(t)=-1有一个根t1,其中0<t1<1,
由f(x)=t1∈(0,1)知此时x只有1个解,
即函数y=f[f(x)]+1有1个零点.
综上:只有③④正确,
故选:D.

练习册系列答案
相关题目




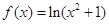 的图象大致是( )
的图象大致是( )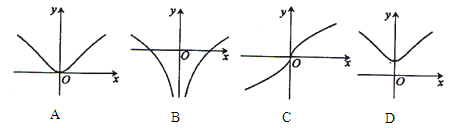
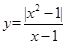 的图象与函数
的图象与函数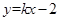 的图象恰有两个交点,则实数
的图象恰有两个交点,则实数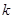 的取值范围是 .
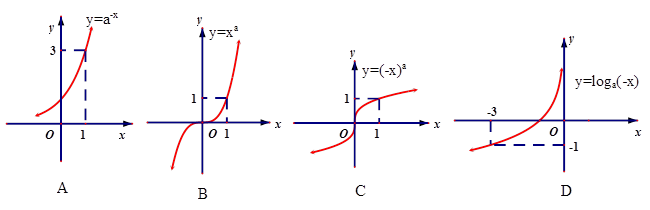
的取值范围是 .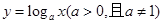 的图像如右图所示,则下列函数图像正确的是( )
的图像如右图所示,则下列函数图像正确的是( )