题目内容
（10分）在锐角△ABC中，a、b、c分别为角A、B、C所对的边，又c＝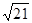
，b＝4，且BC边上的高h＝
。
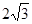（1）求角C；
（2）求边a。
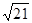，b＝4，且BC边上的高h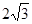＝。（1）求角C；
（2）求边a。
C＝60°，a＝5。
本题注意考查了余弦定理，考查特殊角的三角函数值，属于中档题
①由已知条件，在直角三角形中，利用角C的正弦可求角C；
②在△ABC中，利用余弦定理，结合①得结论可求
解：△ABC为锐角三角形，过A作AD⊥BC于D点，D在线段BC上，
sinC＝
＝
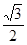，故C＝60°
又由余弦定理知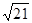：()2＝42＋a2－2×4×a×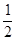
即a2－4a－5＝0 ∴a＝5或a＝－1（舍去）
因此所求角C＝60°，a＝5
①由已知条件，在直角三角形中，利用角C的正弦可求角C；
②在△ABC中，利用余弦定理，结合①得结论可求
解：△ABC为锐角三角形，过A作AD⊥BC于D点，D在线段BC上，
sinC＝
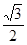＝，故C＝60°又由余弦定理知：(
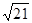)2＝42＋a2－2×4×a×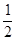即a2－4a－5＝0 ∴a＝5或a＝－1（舍去）
因此所求角C＝60°，a＝5
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
的周长为
,且
的长；
,求角C的度数.
中，已知内角A、B、C所对的边分别为a、b、c，且满足2sinB(2cos2
－1)＝－
cos2B.
，求
的最大值.
所对的边分别为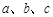
，边a、b是方程x2－2
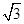x +2=0的两根，角A、B满足关系2sin(A+B)－
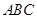中，a，b分别是内角A、B的对边，若
，且
，则△
中，角
的对边分别为
，且
，
，
.求
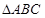中，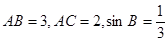
,则符合条件的三角形有（ ）个。
acosB。