题目内容
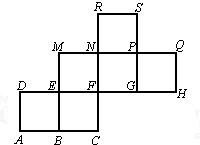
 如图是一个正方体的表面展开图的示意图,MN和PQ是两条面的对角线,请在正方体中将MN和PQ画出来,并就这个正方体解答下列问题.
如图是一个正方体的表面展开图的示意图,MN和PQ是两条面的对角线,请在正方体中将MN和PQ画出来,并就这个正方体解答下列问题.
(1)求MN和PQ所成角的大小;
(2)求四面体M-NPQ的体积与正方体的体积之比.
 解:(1)如图所示,连接BQ、PB,则MN∥BQ,∴∠PQB即为异面直线MN与PQ所成的角.
解:(1)如图所示,连接BQ、PB,则MN∥BQ,∴∠PQB即为异面直线MN与PQ所成的角.又由正方体可知:△PBQ为正三角形,∴∠PQB=60°,
∴异面直线MN与PQ所成的角为60°.
(2)设此正方体的棱长为1,则V正方体QN=1,V三棱锥Q-MNP=
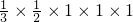 =
= ,
,又∵V三棱锥M-NPQ=V三棱锥Q-MNP,
∴
 =
=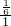 =
= .
.分析:(1)如图所示,连接BQ、PB,则MN∥BQ,所以∠PQB即为异面直线MN与PQ所成的角,进而在正△PBQ中求即可.
(2)利用V三棱锥M-NPQ=V三棱锥Q-MNP,可求出四面体M-NPQ的体积,进而求出答案.
点评:本题考查了正方体中的异面直线所成的角和三棱锥的体积,恰当的转化是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
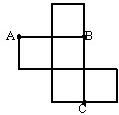 如图,是一个无盖正方体盒子的表面展开图,A、B、C为其上的三个点,则在正方体盒子中,∠ABC=
如图,是一个无盖正方体盒子的表面展开图,A、B、C为其上的三个点,则在正方体盒子中,∠ABC= 如图是一个正方体的表面展开图的示意图,MN和PQ是两条面的对角线,请在正方体中将MN和PQ画出来,并就这个正方体解答下列问题.
如图是一个正方体的表面展开图的示意图,MN和PQ是两条面的对角线,请在正方体中将MN和PQ画出来,并就这个正方体解答下列问题. 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“努”在正方体的后面,那么这个正方体的前面是( )
水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“努”在正方体的后面,那么这个正方体的前面是( )