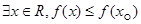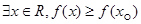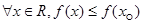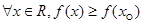题目内容
给出四个命题:①函数是其定义域到值域的映射;②f(x)=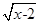 +
+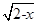 是函数;③函数y=2x(x∈N)的图象是一条直线;④f(x)=
是函数;③函数y=2x(x∈N)的图象是一条直线;④f(x)=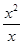 与g(x)=x是同一个函数.其中正确的有 ( )
与g(x)=x是同一个函数.其中正确的有 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
B
解析试题分析:对于①,函数是对于定义域中的每一个值,值域中都有唯一的函数值与之对应,所以函数是定义域到值域的映射,故①正确;对于②,要使f(x)有意义,需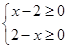 解得x=2,故f(x)是定义域为{2}的函数,故②正确.对于③,函数y=2x(x∈N)的图象是一条直线上的一些孤立的点,故③错;对于④,函数f(x)的定义域为{x|
解得x=2,故f(x)是定义域为{2}的函数,故②正确.对于③,函数y=2x(x∈N)的图象是一条直线上的一些孤立的点,故③错;对于④,函数f(x)的定义域为{x|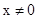 ,x∈R},函数g(x)的定义域为R,故f(x)=
,x∈R},函数g(x)的定义域为R,故f(x)=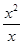 与g(x)=x是同一个函数,故④不正确.综上正确只有①、②两个,故选B
与g(x)=x是同一个函数,故④不正确.综上正确只有①、②两个,故选B
考点:本题考查了函数的概念
点评:函数与映射的关系:函数是特殊的映射;研究函数一定要注意函数的三要素中的定义域非空.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列有关命题的说法正确的是( )
A.命题“若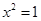 ,则 ,则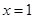 ” 的否命题为“若 ” 的否命题为“若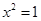 ,则 ,则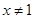 ” ” |
B.“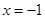 ”是“ ”是“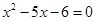 ”的必要而不充分条件 ”的必要而不充分条件 |
C.命题“存在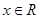 ,使得 ,使得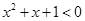 ”的否定是“对任意 ”的否定是“对任意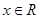 ,均有 ,均有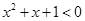 ” ” |
D.命题“若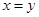 ,则 ,则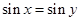 ”的逆否命题为真命题 ”的逆否命题为真命题 |
已知a,b是实数,则“| a+b |=| a |+| b |”是“ab>0”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
“三角形有一个内角为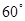 ”是“三内角成等差数列”的( )
”是“三内角成等差数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设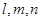 均为直线,其中
均为直线,其中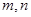 在平面
在平面 内,则
内,则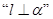 是
是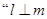 且
且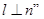 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列命题中正确的是( )
| A.第一象限角必是锐角 | B.终边相同的角相等 |
| C.负角必是第四象限角 | D.相等的角终边必相同 |
下面是关于复数 的三个命题:
的三个命题: 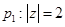
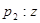 在复平面内对应的点在第四象限
在复平面内对应的点在第四象限 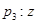 是纯虚数
是纯虚数
其中的真命题为
A.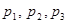 | B.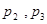 | C.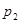 | D.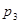 |
下列说法错误的是( )
A.命题:“已知 是 是 上的增函数,若 上的增函数,若 ,则 ,则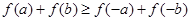 ”的逆否命题为真命题 ”的逆否命题为真命题 |
B.命题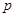 :“存在 :“存在 ,使得 ,使得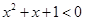 ”,则 ”,则 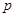 :“任意 :“任意 ,均有 ,均有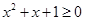 ” ” |
C.若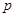 且 且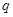 为假命题,则 为假命题,则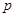 、 、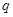 均为假命题 均为假命题 |
D.“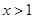 ”是“ ”是“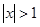 ”的充分不必要条件 ”的充分不必要条件 |
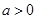 ,函数
,函数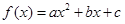 ,若
,若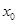 满足关于
满足关于 的方程
的方程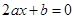 ,则下列选项的命题中为假命题的是( )
,则下列选项的命题中为假命题的是( )