题目内容
已知数列{an}通项为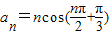
，Sn为其前n项的和，则S2012= ．
【答案】分析：得a1+a2+a3+a4=a5+a6+a7+a8=…=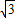
+1，则四项结合的和为定值，可求结果．
解答：解：由于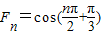
是以4为周期，
∵a1+a2+a3+a4=a5+a6+a7+a8=…=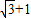
，
∴S2012=a1+a2+a3+a4+…+a2012，
=
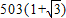
故答案为：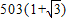
点评：本题主要考查了由数列的通项求解数列的和，解题的关键是由通项发现四项结合为定值的规律
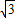+1，则四项结合的和为定值，可求结果．解答：解：由于
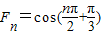是以4为周期，∵a1+a2+a3+a4=a5+a6+a7+a8=…=
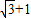，∴S2012=a1+a2+a3+a4+…+a2012，
=
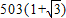
故答案为：
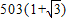
点评：本题主要考查了由数列的通项求解数列的和，解题的关键是由通项发现四项结合为定值的规律
练习册系列答案
相关题目