题目内容
已知数列{an}通项公式为an=λn2+2n+1，求证数列{an}为等差数列的充要条件是λ=0．
分析：根据充要条件的定义和等差数列的定义进行证明即可．
解答：解：充分性：若λ=0，则an=λn2+2n+1=2n+1，
当n≥2时，an-an-1=2n+1-（2n-2+1）=2，为常数，此时数列{an}为等差数列．
必要性：若数列{an}为等差数列，
则当n≥2时，an-an-1=λn2+2n+1-[λ（n-1）2+2（n-1）+1]=3λ+2为常数，则必有3λ=0，即λ=0．
∴数列{an}为等差数列的充要条件是λ=0．
当n≥2时，an-an-1=2n+1-（2n-2+1）=2，为常数，此时数列{an}为等差数列．
必要性：若数列{an}为等差数列，
则当n≥2时，an-an-1=λn2+2n+1-[λ（n-1）2+2（n-1）+1]=3λ+2为常数，则必有3λ=0，即λ=0．
∴数列{an}为等差数列的充要条件是λ=0．
点评：本题主要考查充要条件的证明，根据等差数列的定义是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
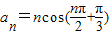，Sn为其前n项的和，则S2012= ．