题目内容
【题目】已知双曲线
，过点
作直线
与双曲线交于
两点，使点
是线段
的中点,那么直线的方程为
A. 
B. 
C. 
D. 不存在
【答案】D
【解析】分析：首先利用直线所过的点将直线方程设出来，要分直线的斜率存在与不存在两种情况，联立消元，化为关于x的一元二次方程，通过有两个交点，得到判别式大于零，求得斜率的取值范围，再借助于中点坐标，结合韦达定理，得到斜率所满足的等量关系式，求得结果后要判断是否在相应的范围内，从而求得结果.
详解：根据题意，设过点
的直线方程为
或
，当
存在时，有
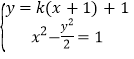，得
（
），当直线与双曲线有两个不同交点时，必有
，解得
，
又方程（）的两个不同的根是两交点
的横坐标，所以
，又
为线段AB的中点，所以
，即
，解得
，不满足，当直线为时不满足条件，所以符合条件的直线
不存在，故选D.
练习册系列答案
相关题目
