题目内容
4．“a=2”是“函数f（x）=x2+3ax-2在区间（-∞，-2]内单调递减”的（ ）| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既非充分又非必要条件 |
分析 先求出关于满足函数$f（x）=x_{\;}^2+3a-2$的条件的a的范围，从而根据a的范围结合充分必要条件判断出结论即可．
解答 解：若函数$f（x）={x}_{\;}^{2}+3ax-2$在区间（-∞，-2]内单调递减，
则有$-\frac{3a}{2}≥-2$，即$a≤\frac{4}{3}$，
所以“a=2”是“函数$f（x）=x_{\;}^2+3a-2$在区间（-∞，-2]内单调递减”的非充分非必要条件，
故选：D．
点评 本题考查了充分必要条件，考查函数的单调性问题，求出f（x）中的a的范围是解题的关键，本题是一道基础题．
练习册系列答案
相关题目
14．下列各组函数f（x）与g（x）的图象相同的是（ ）
| A． | f（x）=$\frac{{{x^2}-4}}{x-2}$，g（x）=x+2 | B． | f（x）=$\sqrt{x^2}，g（x）={（{\sqrt{x}}）^2}$ | ||
| C． | f（x）=$\sqrt{x+1}•\sqrt{x-1}，g（x）=\sqrt{{x^2}-1}$ | D． | f（x）=|x|，g（x）=$\left\{\begin{array}{l}x（x≥0）\\-x（x＜0）\end{array}$ |
12．下列命题中，正确的是（ ）
| A． | 若a＞b，c＞d，则ac＞bd | B． | 若ac＞bc，则a＞b | ||
| C． | 若ac2＜bc2，则a＜b | D． | 若a＞b，c＞d，则a-c＞b-d |
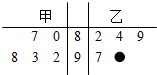下面茎叶图是甲、乙两人在5次综合测评中成绩（所有成绩取整数）的茎叶图，其中一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率为$\frac{4}{5}$．