题目内容
已知M(a,0)为抛物线y2=2px(p>0)的对称轴上的一个动点,在抛物线上求一点N,使得|MN|最小.
解:设抛物线y2=2px(p>0)上一点N(x0,y0),则有y02=2px0,|MN|2=(x0-a)2+y02=x02-2ax0+a2+2px0=[x0-(a-p)]2-p2+2ap.
(1)当a>p时,x0=a-p时,|MN|最小,N的坐标为(a-p,±![]() );
);
(2)当a≤p时,x0=0时,|MN|最小,N的坐标为(0,0).

练习册系列答案
相关题目
 已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.
已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.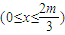 和椭圆弧
和椭圆弧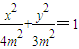

 和椭圆弧
和椭圆弧
