题目内容

设x＞0，y＞0，xy=4，则s=
x2
y
+
y2
x
取最小值时x的值为（　　）
A．1B．2C．4D．8
∵x＞0，y＞0，xy=4，
∴s=
x2
y
+
y2
x
≥2
x2
y
•
y2
x
=2
xy
=4，
当且仅当
x2
y
=
y2
x
时，等号成立
由
x2
y
=
y2
x
，xy=4，得x=y=2．
则s=
x2
y
+
y2
x
取最小值时x的值为2．
故选B．
练习册系列答案
相关题目
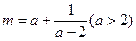已知，n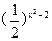＝(x＜0)，则m与n的大小关系为　　　　.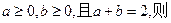
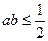
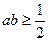
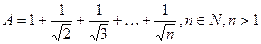
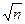一种产品的年产量情况是：第一年为a件，第二年比第一年增长p1%，第三年比第二年增长p2%，且p1＞0，p2＞0，p1＋p2＝2p，如果年平均增长x%，则x,p的大小关系是      。
已知
A．B．C．D．
已知x＞0，y＞0，且（x+1）（y+1）=4，则有xy的最大值为（　　）
A．1B．2C．3D．4
已知4a+5b=20（a＞0，b＞0），则
5
a
+
1
b
的最小值为（　　）
A．
25
6
B．
9
4
C．1D．4
设x，y满足约束条件
x+y≥1
x-y≥-1
2x-y≤2
，若目标函数z=4ax+3by，（a＞0，b＞0）的最大值为12，则
1
a
+
1
b
的最小值为______．
若a，b∈（0，+∞），且a+3b=1，则
3
a
+
1
b
的最小值为（　　）
A．12B．16C．24D．32
设
（1）证明A>;  
（2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网