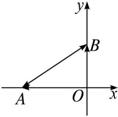
题目内容
如图,已知两点A(-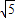 ,0)、B(
,0)、B(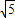 ,0),△ABC的内切圆的圆心在直线x=2上移动.
,0),△ABC的内切圆的圆心在直线x=2上移动.(Ⅰ)求点C的轨迹方程;
(Ⅱ)过点M(2,0)作两条射线,分别交(Ⅰ)中所求轨迹于P、Q两点,且
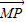
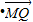 =0,求证:直线PQ必过定点.
=0,求证:直线PQ必过定点.
【答案】分析:(Ⅰ)由题意,根据平面几何知识可知C的轨迹是以A、B为焦点,实轴长为4的双曲线的右支(不含右顶点),
由|CA|-|CB|=|AD|-|BD|求出实半轴,结合b2=c2-a2求出b2,则C点的轨迹可求;
(Ⅱ)设出直线PQ与x轴的交点,由此写出直线PQ所在直线方程,和双曲线方程联立后化为关于y的一元二次方程,利用根与系数关系得到P,Q两点的纵坐标的和与积,结合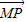
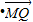 =0列式求出PQ与x轴交点的横坐标为定值.
=0列式求出PQ与x轴交点的横坐标为定值.
解答:解:(Ⅰ)设△ABC内切圆切AB边于点D,
则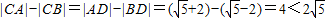 .
.
∴点C的轨迹是以A、B为焦点,实轴长为4的双曲线的右支(不含右顶点),
由a=2,c=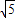 ,得
,得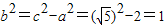 .
.
所以点C的方程为 ;
;
(Ⅱ)设PQ:x=my+a(a>2),代入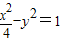 ,
,
得(m2-4)y2+2amy+a2-4=0
设P(x1,y1),Q(x2,y2),
则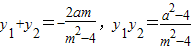 .
.
∵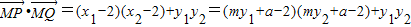
=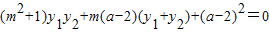 .
.
∴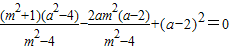 .
.
化简,得3a2-16a+20=0,解得a=2(舍去)或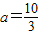 .
.
故直线PQ必过定点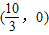 .
.
点评:本题主要考查了直线与圆锥曲线的位置关系的应用,直线与曲线联立,利用方程的根与系数的关系是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是难题.
由|CA|-|CB|=|AD|-|BD|求出实半轴,结合b2=c2-a2求出b2,则C点的轨迹可求;
(Ⅱ)设出直线PQ与x轴的交点,由此写出直线PQ所在直线方程,和双曲线方程联立后化为关于y的一元二次方程,利用根与系数关系得到P,Q两点的纵坐标的和与积,结合
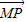
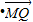 =0列式求出PQ与x轴交点的横坐标为定值.
=0列式求出PQ与x轴交点的横坐标为定值.解答:解:(Ⅰ)设△ABC内切圆切AB边于点D,
则
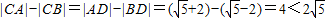 .
.∴点C的轨迹是以A、B为焦点,实轴长为4的双曲线的右支(不含右顶点),
由a=2,c=
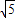 ,得
,得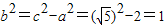 .
.所以点C的方程为
 ;
;(Ⅱ)设PQ:x=my+a(a>2),代入
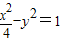 ,
,得(m2-4)y2+2amy+a2-4=0
设P(x1,y1),Q(x2,y2),
则
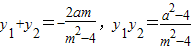 .
.∵
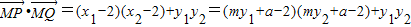
=
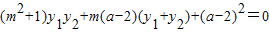 .
.∴
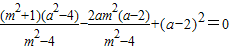 .
.化简,得3a2-16a+20=0,解得a=2(舍去)或
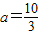 .
.故直线PQ必过定点
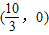 .
.点评:本题主要考查了直线与圆锥曲线的位置关系的应用,直线与曲线联立,利用方程的根与系数的关系是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是难题.

练习册系列答案
相关题目
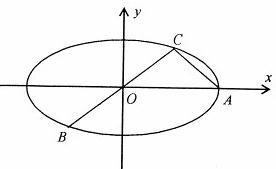 如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且
如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且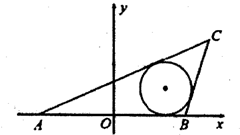 如图,已知两点A(-
如图,已知两点A(-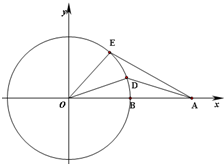 如图,已知点A(2,0),B(1,0),点D,E同时从点B出发沿单位圆O逆时针运动,且点E的角速度是点D的角速度的2倍.设∠BOD=θ,0≤θ<2π
如图,已知点A(2,0),B(1,0),点D,E同时从点B出发沿单位圆O逆时针运动,且点E的角速度是点D的角速度的2倍.设∠BOD=θ,0≤θ<2π