题目内容
曲线A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
解析:因为曲线表示单位圆,其圆心在原点,半径为1,所以曲线上的点到两坐标轴的距离之和不小于1,且不会恒等于1(这是因为直角三角形两直角边之和大于斜边之缘故),故最大值必大于1,排除A,B,C,选D.
答案:D

练习册系列答案
相关题目
在曲线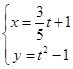 (
(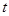 为参数)上的点是( )
为参数)上的点是( )
A.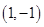 | B.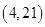 | C.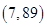 | D.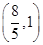 |
题目内容
曲线A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
解析:因为曲线表示单位圆,其圆心在原点,半径为1,所以曲线上的点到两坐标轴的距离之和不小于1,且不会恒等于1(这是因为直角三角形两直角边之和大于斜边之缘故),故最大值必大于1,排除A,B,C,选D.
答案:D

在曲线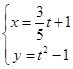 (
(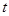 为参数)上的点是( )
为参数)上的点是( )
A.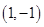 | B.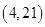 | C.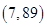 | D.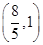 |