题目内容
【题目】图1,平行四边形![]() 中,
中, ![]() ,
, ![]() ,现将
,现将![]() 沿
沿![]() 折起,得到三棱锥
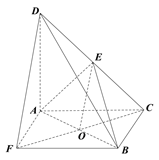
折起,得到三棱锥![]() (如图2),且
(如图2),且![]() ,点
,点![]() 为侧棱
为侧棱![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)在![]() 的角平分线上是否存在点
的角平分线上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(Ⅰ)由平面几何知识先证明![]() ,再由线面垂直的判定的定理可得
,再由线面垂直的判定的定理可得![]() 平面
平面![]() ,从而得
,从而得![]() ,进而可得
,进而可得![]() 平面
平面![]() ,最后由由线面垂直的判定的定理可得结论;(Ⅱ)由等积变换可得
,最后由由线面垂直的判定的定理可得结论;(Ⅱ)由等积变换可得![]() ,进而可得结果;(Ⅱ)取
,进而可得结果;(Ⅱ)取![]() 中点
中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,先证四边形
,先证四边形![]() 为平行四边形,则有
为平行四边形,则有![]() ∥
∥![]() ,利用平面几何知识可得结果.
,利用平面几何知识可得结果.
试题解析:(Ⅰ)证明:在平行四边形![]() 中,有
中,有![]() ,又因为
,又因为![]() 为侧棱
为侧棱![]() 的中点,
的中点,
所以![]() ;
;
又因为![]() ,
, ![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() ;
;
因为![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(Ⅱ)解:因为![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 是三棱锥的高,
是三棱锥的高,
故![]() ,
,
又因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,
,
所以有 ![]() .
.
(Ⅲ)解:取![]() 中点
中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() .
.
因为![]() ,所以射线
,所以射线![]() 是角
是角![]() 的角分线.
的角分线.
又因为点![]() 是的
是的![]() 中点,所以
中点,所以![]() ∥
∥![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() .
.
因为![]() 、
、![]() 互相平分,
互相平分,
故四边形![]() 为平行四边形,有
为平行四边形,有![]() ∥
∥![]() .
.
又因为![]() ,所以有
,所以有![]() ,
,
又因为![]() ,故
,故![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了![]() 至
至![]() 月份每月
月份每月![]() 号的昼夜温差情况与因患感冒而就诊的人数,得到如下数据资料:
号的昼夜温差情况与因患感冒而就诊的人数,得到如下数据资料:
日期 |
|
|
|
|
|
|
昼夜温差 |
|
|
|
|
|
|
就诊人数 |
|
|
|
|
|
|
该兴趣小组确定的研究方案是:先从这![]() 组(每个有序数对
组(每个有序数对![]() 叫作一组)数据中随机选取
叫作一组)数据中随机选取![]() 组作为检验数据,用剩下的
组作为检验数据,用剩下的![]() 组数据求线性回归方程.
组数据求线性回归方程.
(Ⅰ)求选取的![]() 组数据恰好来自相邻两个月的概率;
组数据恰好来自相邻两个月的概率;
(Ⅱ)若选取的是![]() 月和
月和![]() 月的两组数据,请根据
月的两组数据,请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅲ)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过![]() 人,则认为得到的线性回归方程是理想的,试问(Ⅱ)中所得到的线性回归方程是否是理想的?
人,则认为得到的线性回归方程是理想的,试问(Ⅱ)中所得到的线性回归方程是否是理想的?
参考公式: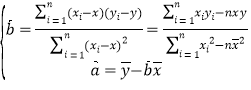 .
.
【题目】为了解高校学生平均每天使用手机的时间长短是否与性别有关,某调查小组随机抽取了25 名男生、10名女生进行为期一周的跟踪调查,调查结果如表所示:
平均每天使用手机 | 平均每天使用手机 | 合计 | |
男生 | 15 | 10 | 25 |
女生 | 3 | 7 | 10 |
合计 | 18 | 17 | 35 |
(I) 根据列联表判断,是否有90%的把握认为学生使用手机的时间长短与性别有关;
(II)在参与调查的平均每天使用手机不超过3小时的10名男生中,有6人使用国产手机,从这10名男生中任意选取3人,求这3人中使用国产手机的人数![]() 的分布列和数学期望.
的分布列和数学期望.
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
参考公式:![]()
![]()
【题目】某超市计划销售某种食品,现邀甲、乙两个商家进场试销5天.两个商家提供的返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利2元;乙商家无固定返利,卖出30件以内(含30件)的食品,每件食品商家返利4元,超出30件的部分每件返利6元.经统计,两个商家的试销情况茎叶图如下:
甲 | 乙 | |||||||
9 | 8 | 9 | 2 | 8 | 8 | |||
2 | 2 | 3 | 2 | 1 | 1 | |||
(1)现从甲商家试销的5天中抽取两天,求这两天的销售量都小于30的概率;
(2)超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日平均返利额的角度考虑,请利用所学的统计学知识为超市作出选择,并说明理由.
