题目内容
如图：一个圆锥的底面半径为2，高为6，在其中有一个半径为x的内接圆柱．
（1）试用x表示圆柱的体积；
（2）当x为何值时，圆柱的侧面积最大，最大值是多少．
（1）试用x表示圆柱的体积；
（2）当x为何值时，圆柱的侧面积最大，最大值是多少．
（1）∵圆锥的底面半径为2，高为6，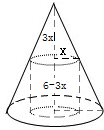
∴内接圆柱的底面半径为x时，它的上底面截圆锥得小圆锥的高为3x
因此，内接圆柱的高h=6-3x；
∴圆柱的体积V=πx2（6-3x）（0＜x＜2）---------------------------（6分）
（2）由（1）得，圆柱的侧面积为
S侧=2πx（6-3x）=6π（2x-x2）（0＜x＜2）
令t=2x-x2，当x=1时tmax=1．可得当x=1时，（S侧）max=6π
∴当圆柱的底面半径为1时，圆柱的侧面积最大，侧面积有最大值为6π．------------------------------（7分）
∴内接圆柱的底面半径为x时，它的上底面截圆锥得小圆锥的高为3x
因此，内接圆柱的高h=6-3x；
∴圆柱的体积V=πx2（6-3x）（0＜x＜2）---------------------------（6分）
（2）由（1）得，圆柱的侧面积为
S侧=2πx（6-3x）=6π（2x-x2）（0＜x＜2）
令t=2x-x2，当x=1时tmax=1．可得当x=1时，（S侧）max=6π
∴当圆柱的底面半径为1时，圆柱的侧面积最大，侧面积有最大值为6π．------------------------------（7分）
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
是空间两条不同直线，
是两个不同平面，下面有四个命题：
②
④
倍，P为侧棱SD上的点。 
是球心
的半径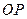
的中点，分别过
作垂直于
