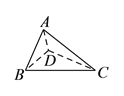��Ŀ����
����Ŀ����֪����f��x��=Asin����x+�գ���x��R������A��0���أ�0��0���գ� ![]() ����ͼ����x��Ľ����У�������������֮��ľ���Ϊ
����ͼ����x��Ľ����У�������������֮��ľ���Ϊ ![]() ����ͼ����һ����ߵ�ΪM��
����ͼ����һ����ߵ�ΪM�� ![]() ��3����
��3����
��1����f��x���Ľ���ʽ��
��2���ȰѺ���y=f��x����ͼ������ƽ�� ![]() ����λ���ȣ�Ȼ���ٰ�����ͼ���ϸ���ĺ������쳤��ԭ����2���������겻�䣩���õ�����y=g��x����ͼ����д������y=g��x���Ľ���ʽ��
����λ���ȣ�Ȼ���ٰ�����ͼ���ϸ���ĺ������쳤��ԭ����2���������겻�䣩���õ�����y=g��x����ͼ����д������y=g��x���Ľ���ʽ��
��3���ڣ�2���������£����ܴ���x0��[�� ![]() ��
�� ![]() ]��ʹ�ò���ʽg��x0��+2��log3m��������ʵ��m����Сֵ��
]��ʹ�ò���ʽg��x0��+2��log3m��������ʵ��m����Сֵ��
���𰸡�
��1���⣺�� ![]() T=
T= ![]() ��
��
��T= ![]() =�У���æ�=2��
=�У���æ�=2��
�ֺ���f��x��=Asin��2x+�գ�ͼ����һ����ߵ�ΪM�� ![]() ��3����
��3����
��A=3��2�� ![]() +��=2k��+
+��=2k��+ ![]() ��k��Z����
��k��Z����
���=2k��+ ![]() ��k��Z������0���գ�
��k��Z������0���գ� ![]() ��
��
���= ![]() ��
��
��f��x��=3sin��2x+ ![]() ��
��
��2���⣺�Ѻ���y=f��x����ͼ������ƽ�� ![]() ����λ���ȣ��õ�f��x+
����λ���ȣ��õ�f��x+ ![]() ��=3sin[2��x+
��=3sin[2��x+ ![]() ��+
��+ ![]() ]=3cos2x��
]=3cos2x��
Ȼ���ٰ�����ͼ���ϸ���ĺ������쳤��ԭ����2���������겻�䣩���õ�����y=g��x��=3cosx��ͼ��
��g��x��=3cosx
��3���⣺��x0��[�� ![]() ��
�� ![]() ]���ੁ
]���ੁ ![]() ��cosx0��1����
��cosx0��1���� ![]() ��3cosx0��3��
��3cosx0��3��
������֪��log3m�ݣ��� ![]() ��+2=
��+2= ![]() ��
��
��m�� ![]() ����ʵ��m����СֵΪ
����ʵ��m����СֵΪ ![]()
����������1��������֪ ![]() T=
T= ![]() ���ɴ˿���æ�=2���ֺ���f��x��=Asin��2x+�գ�ͼ����һ����ߵ�ΪM��
���ɴ˿���æ�=2���ֺ���f��x��=Asin��2x+�գ�ͼ����һ����ߵ�ΪM�� ![]() ��3������֪A=3��2��
��3������֪A=3��2�� ![]() +��=2k��+
+��=2k��+ ![]() ��k��Z�������0���գ�
��k��Z�������0���գ� ![]() ����æգ��Ӷ��ɵ�f��x���Ľ���ʽ����2�����ú���y=Asin����x+�գ���ͼ��任����ú���y=g��x���Ľ���ʽ����3��x0��[��
����æգ��Ӷ��ɵ�f��x���Ľ���ʽ����2�����ú���y=Asin����x+�գ���ͼ��任����ú���y=g��x���Ľ���ʽ����3��x0��[�� ![]() ��
�� ![]() ]��
]�� ![]() ��cosx0��1����
��cosx0��1���� ![]() ��3cosx0��3��������֪��log3m�ݣ���
��3cosx0��3��������֪��log3m�ݣ��� ![]() ��+2=
��+2= ![]() ���Ӷ������ʵ��m����Сֵ��
���Ӷ������ʵ��m����Сֵ��
�����㾫�������ú���y=Asin����x+�գ���ͼ��任����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪ͼ�������е������ң�ƽ��![]() ����λ���ȣ��õ�����
����λ���ȣ��õ�����![]() ��ͼ���ٽ�����
��ͼ���ٽ�����![]() ��ͼ�������е�ĺ������쳤�����̣���ԭ����
��ͼ�������е�ĺ������쳤�����̣���ԭ����![]() ���������겻�䣩���õ�����
���������겻�䣩���õ�����![]() ��ͼ���ٽ�����
��ͼ���ٽ�����![]() ��ͼ�������е���������쳤�����̣���ԭ����
��ͼ�������е���������쳤�����̣���ԭ����![]() ���������겻�䣩���õ�����
���������겻�䣩���õ�����![]() ��ͼ��
��ͼ��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��Ϊ�˽�ij����ѧ���Ͱ�����ʦ���ҳ����ڵ������ʿ�Ը߿�Ӣ��ĸ�Ŀ�����ijý���ڸõ���ѡ����3600�˵��飬���Ƿ���ȡ��Ӣ�������������⣬����ͳ�ƵĽ�����±���
![]()
| Ӧ��ȡ�� | Ӧ�ñ��� | ����ν | |
��Уѧ�� | 2100�� | 120�� | y�� | |
�����ʿ | 600�� | x�� | z�� |
��֪��ȫ�������������ȡ1�ˣ��鵽����Ӧ�ñ�����̬�ȵ��˵ĸ���Ϊ0.05��
��1�����÷ֲ�����ķ��������в����������г�ȡ360�˽����ʾ���̸����Ӧ�ڳ�������ν��̬�ȵ����г�ȡ�����ˣ�
��2���ڳ���Ӧ�ñ�����̬�ȵ����У��÷ֲ�����ķ�����ȡ6��ƽ���ֳ�����������뽻�������һ������Уѧ���������ķֲ��к���ѧ������