题目内容
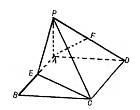
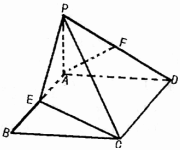
 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.(1)求证:AF∥平面PCE;
(2)若二面角P-CD-B为45°,AD=2,CD=3,求点F到平面PCE的距离;
(3)在(2)的条件下,求PC与底面所成角的余弦值.
分析:(1)取PC中点M,连结ME、MF,可证得四边形AFME是平行四边形,则AF∥EM,由线面平行的判定定理可得AF∥平面PCE;
(2)以A为坐标原点,分别以AE、AD、AP所在直线为x、y、z轴建立坐标系,求出平面PCE的法向量为
═(4,-3,3),将
=(0,1,-1)代入点F到平面PCE的距离为d=
,可得点F到平面PCE的距离;
(3)由PA⊥平面ABCD,可得AC是PC在底面上的射影,即∠PCA就是PC与底面所成的角.求出向量
,
,代入向量夹角公式,可得答案.
(2)以A为坐标原点,分别以AE、AD、AP所在直线为x、y、z轴建立坐标系,求出平面PCE的法向量为
| n |
| PF |
|
| ||||
|
|
(3)由PA⊥平面ABCD,可得AC是PC在底面上的射影,即∠PCA就是PC与底面所成的角.求出向量
| CA |
| CP |
解答: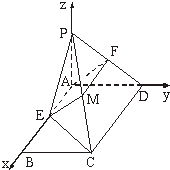 证明:(1)取PC中点M,连结ME、MF,
证明:(1)取PC中点M,连结ME、MF,
则MF∥CD,MF=
CD.
又AE∥CD,AE=
CD,
∴AE∥MF且AE=MF.
∴四边形AFME是平行四边形.
∴AF∥EM.
∵AF?平面PCE,EM?平面PCE,
∴AF∥平面PCE.
(2)解:以A为坐标原点,分别以AE、AD、AP所在直线为x、y、z轴建立坐标系.
∵PA⊥平面AC,CD?平面AC
∴PA⊥CD
又∵CD⊥AD,PA∩AD=A,PA,AD?平面PAD
∴CD⊥平面PAD
又∵PD?平面PAD
∴CD⊥PD.
∴∠PDA是二面角P-CD-B的平面角,即∠PDA=45°.
∴A(0,0,0)、P(0,0,2)、D(0,2,0)、F(0,1,1)、E(
,0,0)、C(3,2,0).
设平面PCE的法向量为
=(x,y,z),
则
⊥
,
⊥
,而
=(-
,0,2),
=(
,2,0),
∴-
x+2z=0,且
x+2y=0.
取x=4,得
=(4,-3,3).
又
=(0,1,-1),
故点F到平面PCE的距离为d=
=
解:(3)∵PA⊥平面ABCD,
∴AC是PC在底面上的射影.
∴∠PCA就是PC与底面所成的角.
=(-3,-2,0),
=(-3,-2,2).
∴cos∠PCA=
=
,
即PC与底面所成的角的余弦值是
 证明:(1)取PC中点M,连结ME、MF,
证明:(1)取PC中点M,连结ME、MF,则MF∥CD,MF=
| 1 |
| 2 |
又AE∥CD,AE=
| 1 |
| 2 |
∴AE∥MF且AE=MF.
∴四边形AFME是平行四边形.
∴AF∥EM.
∵AF?平面PCE,EM?平面PCE,
∴AF∥平面PCE.
(2)解:以A为坐标原点,分别以AE、AD、AP所在直线为x、y、z轴建立坐标系.
∵PA⊥平面AC,CD?平面AC
∴PA⊥CD
又∵CD⊥AD,PA∩AD=A,PA,AD?平面PAD
∴CD⊥平面PAD
又∵PD?平面PAD
∴CD⊥PD.
∴∠PDA是二面角P-CD-B的平面角,即∠PDA=45°.
∴A(0,0,0)、P(0,0,2)、D(0,2,0)、F(0,1,1)、E(
| 3 |
| 2 |
设平面PCE的法向量为
| n |
则
| n |
| EP |
| n |
| EC |
| EP |
| 3 |
| 2 |
| EC |
| 3 |
| 2 |
∴-
| 3 |
| 2 |
| 3 |
| 2 |
取x=4,得
| n |
又
| PF |
故点F到平面PCE的距离为d=
|
| ||||
|
|
3
| ||
| 17 |
解:(3)∵PA⊥平面ABCD,
∴AC是PC在底面上的射影.
∴∠PCA就是PC与底面所成的角.
| CA |
| CP |
∴cos∠PCA=
|
| ||||
|
|
| ||
| 17 |
即PC与底面所成的角的余弦值是
| ||
| 17 |
点评:本题考查的知识点是线面平行的判定定理,点到平面的距离,二面角,线面夹角,其中(1)的关键熟练掌握线面平行的判定定理,解答(2)(3)的关键是建立空间坐标系,将二面角及线面夹角问题转化为空间向量夹角问题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.