题目内容
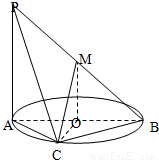
如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:(1)PA∥平面MOB; (2)MO∥平面PAC;
(3)OC⊥平面PAB; (4)平面PAC⊥平面PBC,
其中正确的命题是 .
【答案】分析:利用直线与平面是否在平面内,判断(1)的正误;
利用直线与平面的平行证明MO∥平面PAC;判断它的正误即可;
利用直线OC是否垂直平面内的两条相交直线,即可判断(3)的正误;
利用平面与平面垂直的判定定理判断(4)的正误;
解答: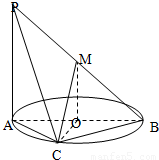 解:由题意可知PA⊥平面ABC,点M为线段PB的中点,O是圆的圆心,所以MO⊥平面ABC,PA∥OM,所以PA与MO共面,(1)不正确;
解:由题意可知PA⊥平面ABC,点M为线段PB的中点,O是圆的圆心,所以MO⊥平面ABC,PA∥OM,所以PA与MO共面,(1)不正确;
又PA∥OM,OM?平面PAC,PA?平面PAC,∴MO∥平面PAC;(2)正确;
因为AB为圆O的直径,点C在圆周上(异于A,B点),所以OC不垂直AC,所以OC⊥平面PAB;不正确;
因为AB为圆O的直径,点C在圆周上(异于A,B点),所以BC⊥AC,∵直线PA垂直于圆所在的平面,∴BC⊥PA,可知BC⊥平面PAC,BC?平面PBC,所以平面PAC⊥平面PBC,
(4)正确.
故答案为:(2)(4).
点评:本题考查直线与直线的平行,直线与平面的平行与垂直的证明,考查基本知识的应用,空间想象能力,逻辑推理能力.
利用直线与平面的平行证明MO∥平面PAC;判断它的正误即可;
利用直线OC是否垂直平面内的两条相交直线,即可判断(3)的正误;
利用平面与平面垂直的判定定理判断(4)的正误;
解答:
 解:由题意可知PA⊥平面ABC,点M为线段PB的中点,O是圆的圆心,所以MO⊥平面ABC,PA∥OM,所以PA与MO共面,(1)不正确;
解:由题意可知PA⊥平面ABC,点M为线段PB的中点,O是圆的圆心,所以MO⊥平面ABC,PA∥OM,所以PA与MO共面,(1)不正确;又PA∥OM,OM?平面PAC,PA?平面PAC,∴MO∥平面PAC;(2)正确;
因为AB为圆O的直径,点C在圆周上(异于A,B点),所以OC不垂直AC,所以OC⊥平面PAB;不正确;
因为AB为圆O的直径,点C在圆周上(异于A,B点),所以BC⊥AC,∵直线PA垂直于圆所在的平面,∴BC⊥PA,可知BC⊥平面PAC,BC?平面PBC,所以平面PAC⊥平面PBC,
(4)正确.
故答案为:(2)(4).
点评:本题考查直线与直线的平行,直线与平面的平行与垂直的证明,考查基本知识的应用,空间想象能力,逻辑推理能力.

练习册系列答案
相关题目
 如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:
如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题: 如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:其中正确的命题是
如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:其中正确的命题是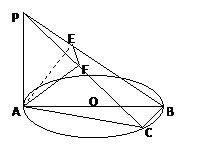
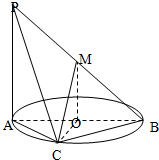 如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:
如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题: