题目内容

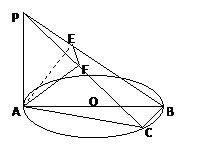
如图,AB为圆O的直径,点C为圆O上异于A、B的一点，PA⊥平面ABC，点A在PB、PC上的射影分别为点E、F.

⑴求证：PB⊥平面AFE；

⑵若AB=4，PA=3，BC=2，求三棱锥C-PAB的体积与此三棱锥的外接球（即点P、A、B、C都在此球面上）的体积之比.

（1）见解析（2）

解析:

⑴

，又AB是圆O的直径,

所以BC⊥面PAC, 又因AF面PAC,

所以AF⊥BC, 又因AF⊥PC,

所以AF⊥面PBC, 又因PB面PBC,

所以PB⊥AF, 又因PB⊥AE, 所以PB⊥面AFE.

⑵，

取PB的中点M，由直角三角形性质得，PM=AM=BM=CM，故三棱锥的外接球球心为M，其半径为，所以，体积之比为

练习册系列答案

新课堂单元达标活页卷系列答案

学考2加1系列答案

国华图书学业测评系列答案

志鸿优化赢在课堂系列答案

作业辅导系列答案

第一课堂课堂作业系列答案

金牌堂堂练系列答案

一本搞定系列答案

同步学典一课多练系列答案

名师金典BFB初中课时优化系列答案

相关题目

（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A₁B₁C₁D₁，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．

（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．

（本小题满分12分）如图，AB为圆O的直

径，点E、F在圆O上，AB∥EF，矩形ABCD

所在的平面和圆O所在的平面垂直，且.

⑴求证：；

⑵设FC的中点为M，求证：；

⑶设平面CBF将几何体分成的两个锥体的体积分别为，求的值.

（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A₁B₁C₁D₁，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．

（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．

（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A₁B₁C₁D₁，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．

（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．

A．（参数方程与极坐标）

直线与直线的夹角大小为

B．（不等式选讲）要使关于x的不等式在实数

范围内有解，则A的取值范围是

C．（几何证明选讲）如图所示，在圆O中，AB是圆O的直

径AB =8,E为OB．的中点，CD过点E且垂直于AB,

EF⊥AC,则

CF•CA=